Aula-3

Aula -3
A Luz como um Fenômeno Eletromagnético

1 - Relação Energia-Momento Linear

Uma partícula movendo-se em um meio resistivo sofrerá forças de oposição ao movimento. Em mecânica, estas forças denominadas de forças de atrito, são dependentes da velocidade de um dado corpo. Usando argumentos semelhantes ao da mecânica, vamos estudar as forças exercidas em superfícies condutoras, por uma radiação eletromagnética (EM).
Para entender este problema vamos analisar a interação de uma onda eletromagnética com um condutor. Isto é, analisaremos o choque de uma onda eletromagnética com uma placa condutora. Veja Fig.1.

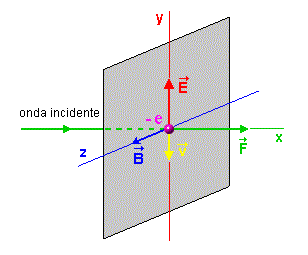
Fig. 1 - Uma onda luminosa inside sobre uma placa condutora

O campo elétrico devido a onda eletromagnética, ao interagir com os elétrons livres do condutor, vai produzir uma força sobre eles do tipo F = eE. Esta força fará com que os elétrons movam-se com um certa velocidade v no interior do condutor, provocando assim o aparecimento de pequenas correntes localizadas. Sabemos também, que adicionalmente aparecerão forças magnéticas como conseqüência do movimento dos elétrons na presença do campo magnético, existente em uma onda eletromagnética. Assim as forças envolvidas são do tipo;

Por outro lado, sabemos que o movimento dos elétrons, no condutor, vai produzir uma força de atrito devido aos choques dos elétrons com as outras partículas na placa condutora. Estas forças de atrito ou de viscosidade, neste caso, são em geral proporcionais à velocidade da partícula no meio, isto é,

onde v é a velocidade dos elétrons e b é a constante de amortecimento. Comparando esta força com a força elétrica, podemos encontrar um relação para a velocidade do elétron em função do campo, isto é,

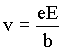Substituindo esta velocidade na equação para a força magnética temos que

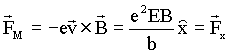A força F_M, sobre o elétron tem o sentido de x, sendo perpendicular ao plano formado pelos vetores v e B, isto é, ao plano yz. Veja Fig. 1.
De acordo com a segunda lei de Newton, F_x é igual a taxa de variação do momento linear com o tempo, isto é

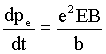O momento linear é transmitido, a esta taxa, a todos os elétrons da lâmina e conseqüentemente à própria lamina. Isto significa uma força resultante não nula, empurrando a lâmina na direção x.
Resta, agora, relacionar a transferência de momento linear com a absorção de energia pela a mesma. A componente elétrica da onda incidente realiza trabalho sobre cada elétron oscilante à taxa de

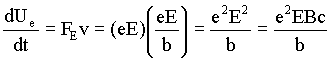onde temos usado a relação E = Bc . Note-se que a força magnética F_x, sendo sempre ortogonal à velocidade v, não realiza trabalho sobre o elétron oscilante.

2- O Princípio de Fermat e o Princípio de Mínima Ação

Em agosto de 1657, o matemático francês Pierre Fermat (1601-1665) escreveu uma carta (Epistolae 42) a Monsieur Cureau de la Chambre, na qual enunciou o seu famoso Princípio do Tempo Mínimo: A Natureza sempre escolhe os menores caminhos. De acordo com esse princípio, observou Fermat, a luz sempre leva o menor tempo para seguir a sua trajetória. Na notação atual, esse Princípio significa dizer que a integral

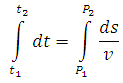
assume um valor mínimo quando a luz viaja com a velocidade v, entre os pontos P₁ e P₂.

Veja o texto de Feynmann sobre o princípio de mínima ação. Click aqui.
Embora tal princípio já fosse do conhecimento do filósofo grego Aristóteles de Siracusa (384-322), de haver sido utilizado pelo matemático e inventor grego Heron de Alexandria (c. 20 A.D.- ? ) e, mais tarde, pelo físico e matemático iraquiano Abu-´Ali Al-Hasan Ibn Al-Haytham (Al-Hazen) (c. 965-1038) na explicação da Lei da Reflexão da Luz, foi Fermat quem, em 1661, a utilizou para demonstrar a Lei da Refração da Luz [Morris Kline, Mathematical Thought from Ancient to Modern Times (Oxford University Press, 1972); Sir Edmund Whittaker, A History of the Theories of Aether and Electricity (Thomas Nelson and Sons, 1952)].

Por outro lado, em 1744 (Mémoires de l´Academie des Sciences de Paris, p. 417), o matemático francês Pierre Louis Moureau de Maupertuis (1698-1759) formulou o Princípio da Mínima Ação: Quando há qualquer mudança na Natureza, a quantidade de ação necessária para essa mudança, é a menor possível. Ele postulou que a ação dependia da massa (m), da velocidade (v) e da distância (s) percorrida por um corpo, ou seja: ação = m v s. Note-se que Maupertuis chegou a esse princípio, tentando encontrar uma base racional e metafísica entre a Óptica Geométrica e a Mecânica Newtoniana [Wolfgang Yourgrau and Stanley Mandelstam, Variational Principles in Dynamics and Quantum Theory (Dover, 1979)]. Ainda em 1744, o matemático suíço Leonard Euler (1707-1783) publicou o livro intitulado Methodus inveniendi lineas curvas maximi minimae proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (“Um método de descobrir linhas curvas que apresentam a propriedade de máximo ou mínimo ou a solução do problema isoperimétrico tomado em seu sentido mais amplo”), escreveu o Princípio de Maupertuis da seguinte forma (em notação atual):

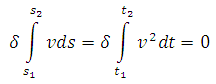É interessante destacar que, além de razões físicas, Maupertuis e Euler alegavam razões teológicas para justificar esse Princípio, pois, diziam eles, as leis do comportamento da Natureza possuem a perfeição digna da criação de Deus.

Observando os dois Princípios, de Fermat e de Maupertuis-Euler, vê-se que, no primeiro, a velocidade aparece inversamente, enquanto no segundo, diretamente relacionada ao deslocamento (ds). Em virtude disso, durante muito tempo não se conseguiu encontrar uma analogia entre tais Princípios. Contudo, com os trabalhos desenvolvidos pelos matemáticos, o irlandês Sir William Rowan Hamilton (1805-1865), em 1835 (Philosophical Transactions of the Royal Society of London, Part II, p. 247) e o alemão Carl Gustav Jacob Jacobi (1804-1851), em 1837 (Journal für Reine und Angewandte Mathematik 17, p. 97), foi possível encontrar a analogia referida acima. Em seu trabalho, Hamilton havia obtido um par de equações diferenciais – as famosas Equações de Hamilton – envolvendo o hoje conhecido operador Hamiltoniano H = E = T + V, isto é, a energia total (E) é igual a soma da energia cinética (T) e da energia potencial (V), partindo de um princípio variacional que havia deduzido no ano anterior, qual seja:

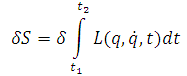
onde S é a conhecida ação Hamiltoniana e L representa o operador Lagrangeano, definido por L = T – V e que havia sido introduzido pelo matemático francês Siméon Denis Poisson (1781-1840), em 1809 (Journal de l´Ecole Polytechnique 8, p. 266). Foi ainda nesse trabalho que Poisson apresentou a definição do momento canonicamente conjugado p

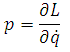
onde q é a coordenada generalizada Lagrangeana e é a velocidade generalizada Lagrangeana). Por seu lado, Jacobi partiu das Equações de Hamilton e encontrou uma nova equação – a conhecida Equação de Hamilton-Jacobi, dada por:

De posse dessa equação, Jacobi encontrou a função S para muitos problemas mecânicos. Por exemplo, considerando sistemas físicos para os quais H(p,q) não depende explicitamente do tempo t, ele mostrou que:

onde E é a energia do sistema físico e W é a função característica de Hamilton. Ainda usando essa solução, Jacobi demonstrou que:

. Este último resultado significa que o momento p é perpendicular à superfície de W [= S₀ (t= 0)] constante. Por outro lado, essa equação é semelhante à Equação Eikonal da Óptica Geométrica, ou seja:

onde G é chamada de eikonal (do grego eikon, que significa imagem) e n é o índice de refração, que varia de posição, isto é: n(r). Registre-se que as superfícies em que G é constante são superfícies de fase óptica constante e, portanto, define frentes de ondas luminosas, cujos raios luminosos correspondentes a essas frentes de ondas lhe são perpendiculares. Essa semelhança ficou conhecida como a Analogia Mecânico-Óptica.

Da formulação de Fermat pode-se mostrar que a óptica geométrica se baseia em três princípios:

   i)- A luz se propaga em linha reta numa região uniforme
   ii)- O ângulo de incidência de um raio luminoso, em espelho, é igual ao ângulo de reflexão
   iii)- Pela lei de Snell os ângulos de incidência e o de refração de um raio luminoso, ao atravessar meios

materiais com índices de refração distintos é dado por : n₁ sen q ₁ = n₂ sen q ₂ .

Mostraremos, a seguir, como estas três regras podem ser obtidas de único princípio da física, conhecido com o princípio de Fermat : A luz para ir de um ponto A a um outro ponto B, o fará pela trajetória cujo tempo de trânsito será menor do que o tempo de trânsito para qualquer outra trajetória vizinha. O princípio de Pierre Fermat foi enunciado por volta de 1650.

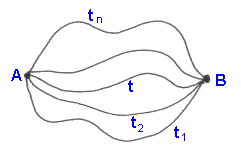
Fig.2- Trajetória de tempo mínimo de acordo com o princípio de Fermat, para um meio homogêneo.

3- A Reflexão

Em seções anteriores, estudamos o processo de reflexão de um raio luminoso, usando o princípio de Huygens juntamente com considerações geométricas. A seguir, estudaremos o mesmo fenômeno usando o princípio de Fermat.

Observando a figura 3(a) notamos que existem várias trajetórias possíveis, para um raio luz ir do ponto A ao B por reflexão no plano espelhar. Neste caso, qual será o caminho realmente percorrido pela luz?

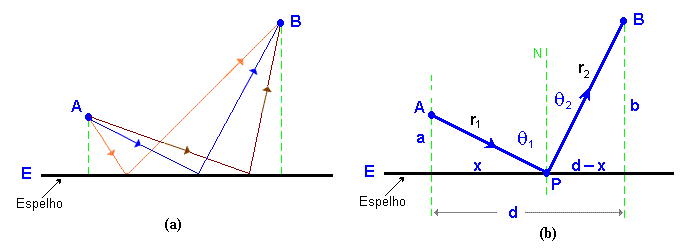
Fig.3- Reflexão da luz por um espelho

De acordo com o princípio de Fermat, um raio de luz percorre o trajeto entre dois pontos levando sempre o menor tempo possível. Com base nisto, responderemos a questão anterior. A figura 3(b) e o teorema de Pitágoras mostram que o comprimento do trajeto de A até o ponto (P) de reflexão no espelho, é

e que o comprimento do trajeto até o ponto B é igual

O tempo de trânsito para ir de A até B é a soma dos tempos gastos pelos raios incidentes e refletidos;

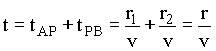
No caso da luz se propagando com velocidade v ao longo do trajeto de A a B, o tempo gasto necessário é o comprimento total do trajeto dividido por v. Assim,

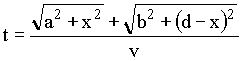
Como o valor de t depende "suavemente" (não há variações abruptas) do valor de x, o cálculo diferencial nos diz que, se houver um valor de x que minimize t, então dt/dx será igual a zero. Logo, calcularemos a derivada, de acordo com Fermat, obtendo.

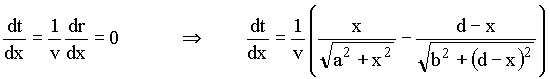
Igualando a derivada a zero, resulta

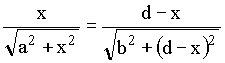
O lado esquerdo dessa igualdade é exatamente sen(q₁) , e o lado direito é exatamente sen(q₂). Portanto temos que sen q ₁ = sen q₂.

Isto significa que, na reflexão o ângulo de incidência é igual ao ângulo de reflexão.

A relação dt/dx = 0 é o critério de que t seja mínimo ou um máximo para o valor de x tirado da relação. Você pode confirmar que o valor obtido para x, na verdade dá um t mínimo calculando esse t e comparando-o com o valor de t obtido para x = 0 e x = r.

4- A Refração

Para deduzir a lei da refração, usando o princípio de Fermat, construímos a Fig. 4, como plano contendo a trajetória da luz perpendicular ao plano que separa as regiões de índices de refração n₁ e n₂. A luz propaga-se do ponto A na primeira região para um ponto a uma distância desconhecida x da base da perpendicular ao plano de separação entre os dos meios materiais. O comprimento da perpendicular é a. A luz continua o seu caminho na Segunda região até B, que está a um ponto B, situado a uma distância b do plano de separação.

De forma similar ao caso da reflexão, existem várias trajetórias possíveis para raio de luz ser refratado ao percorrer por dois meios materiais distintos, como mostra a Fig. 4.

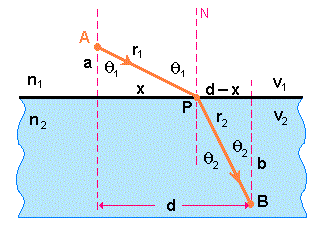
Fig.4- Refração da luz ao atravessar dois meios materiais transparentes e distintos

O tempo para percorrer do ponto A até B, é igual a soma dos tempos para percorrer de A até a superfície P e de P a B. Como os meios têm índice de refração distintos, a luz terá conseqüentemente velocidades diferentes. Seja estas velocidades no meio 1 e 2, iguais a v₁ e v₂ respectivamente. Assim,

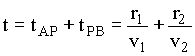
Usando a definição de índice de refração para um meio material em relação ao vácuo temos que,

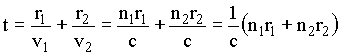
Observando a Fig. 4, por considerações geométricas tiramos que,

Portanto o tempo necessário para a luz se propagar ao longo do trajeto A e B é,

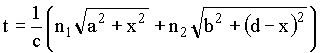
Calculando novamente dt/dx, obtemos

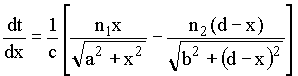
De acordo como princípio de Fermat a trajetória real a ser percorrida pelo raio de luz será aquela que satisfaz a relação dt/dx = 0. Isto significa que,

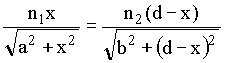
Usando relações geométricas tiradas da Fig. 4, podemos rescrever a equação acima em termos dos ângulos de incidência q ₁ e refração q₂, como a seguir,

Esta equação é a própria lei de Snell, obtida em seções anteriores usando o princípio de Huygens e considerações geométricas.

As afirmações que se seguem dão um resumo qualitativo do fenômeno da refração: Quando um feixe de luz atravessa uma superfície passando para uma região de índice de refração maior, ele se curva aproximando-se da normal à superfície. Quando um feixe de luz atravessa uma superfície passando para uma região de índice menor, ele é encurvado, afastando-se da normal á superfície. Este fenômeno é uma conseqüência da reversibilidade dos raios luminosos em um processo de refração, ou reversibilidade da lei de Snell.

Devemos ressaltar que os fenômenos de reflexão e refração podem ocorrer simultaneamente. Isto significa que parte dos raios luminosos serão refletidos pela superfície de contato e a outra parte refratada. Neste caso, tanto a reflexão quanto a refração continuam obedecendo as leis encontradas anteriormente.

Refração da Luz

by Phillip Dukes @ Brigham Young University, Department of Physics and Astronomy
Modo de usar

A variação do ângulo incidente é de 0 à 85 graus. Pode-se variá-lo de 5 em 5 graus usando os botões +-. O índice de fração do meio superior é n=1 (vácuo). O índice de refração do meio 2 pode ser variado, usando o botão, de n=1.00 (vácuo) até n=2,42 (diamante). O comprimento da onda incidente pode ser variado a partir de 475 nm até 650nm de 15 em 15 nm. Use o botão para incrementá-lo. Note que o comprimento da onda refratada é diminuido por um fator de 1/n

9- Interferência por Difração

A seguir ilustraremos o caso interferência por difração em fendas estreitas. A Fig.5 mostra uma representação esquemática deste caso. Quando a fenda não for estreita, a intensidade da luz em um anteparo distante da fenda não é independente do ângulo de incidência q mas diminui quando o ângulo q aumenta. Vamos considerar uma fenda com a largura a. A Fig.5 mostra a distribuição de intensidade sobre um anteparo bastante afastado da fenda de largura a, em função do ângulo q . Podemos ver que a intensidade é máxima na direção vertical, sen(q ) = 0 e diminui até zero em ângulo que depende da largura a da fenda e do comprimento de onda l . A maior parte da intensidade da luz está concentrada em uma região central bastante larga, embora existam máximos secundários nos dois lados do máximo central.

Veja demonstrações mais detalhadas no Apêndice-3 a seguir.

Fig. 5 - Difração por uma única fenda

Mode de usar: use o mouse para mover o botão do
comprimento de onda e a abertura da fenda

Apêndices
Selecione com o "mouse" o item que lhe interessa.

- Apêndice 2 : Transporte de Energia em Ondas Eletromagnéticas

- Apêndice 3 : Interferência e Difração de Ondas Esféricas

O conteúdo desta página está em constante atualização.
Correções no texto esugestões serão bem vindas.