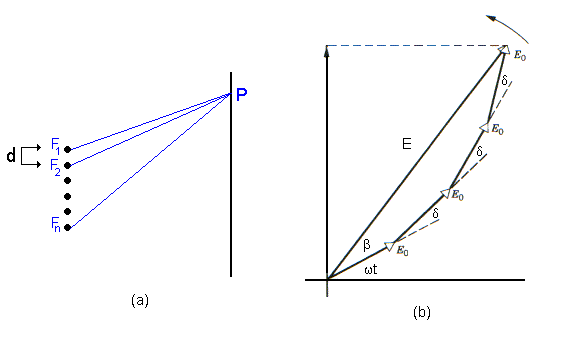
Fig16.1 Conjunto de n-fontes em paralelo
Ondas
Interferência
para o caso de n-fontes
Difração
de Fraunhoffer
Difração
por N-fendas ou Rede de Difração
Simulação
16.1- Interferência para o caso de n-fontes
Na seção anterior estudamos o caso da interferência por duas fontes infinitesimais a qual é algumas vezes denominada por interferência de Young. Nesta seção, estenderemos este conceito para o caso de n-fontes puntiformes.
Se tivermos três ou mais fontes igualmente
espaçadas, e em fase, a figura de interferência em um
anteparo situado longe das fontes tem certa semelhança com à
figura obtida para o caso de duas fontes. As posições dos
máximos de intensidade, no anteparo, são as mesmas quaisquer
que sejam as fontes, mas estes máximos têm muito maior intensidade
e são muito mais nítidos, quando muito mais fontes forem
usadas.
Com base nos mesmos princípios usados para
calcular o intensidade luminosa (I), no caso de duas fontes, podemos também
determiniar uma equação para I no caso de interferência
produziada por três ou mais fontes igualmente espaçadas.

A Fig.16.1, mostra um conjunto de n-fontes em paralelo. Cada uma destas fontes produz, no ponto P, um campo elétrico. A intensidade luminosa total pode ser encontrada calculando o campo elétrico resultante no ponto P. Os campos elétricos produzidos pelas n-fontes são representados pelas equações;
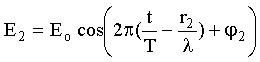
:
:
O campo elétrico resultante, no ponto P, é dado pela soma;
No caso do campo produzido por uma única fonte temos, por analogia que
Das equações anteriores obtemos que
A intensidade luminosa no ponto P, pode ser calculada por,
onde
Supomos que as fontes são eqüidistantes e d é a distância entre elas.
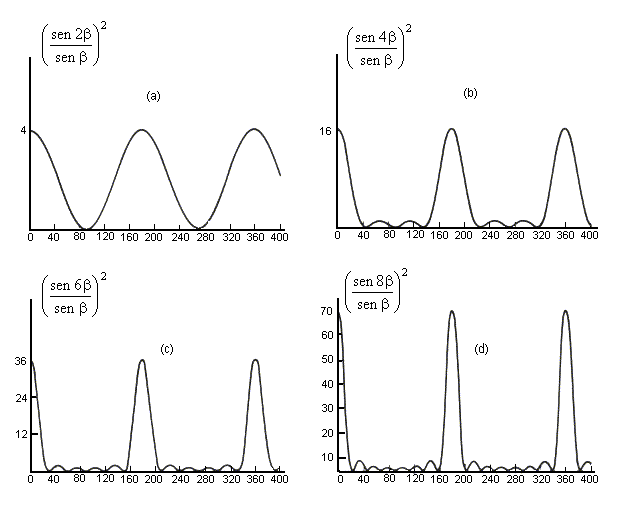
Em seções anteriores discutimos a interferência de Young para duas ou mais fendas. Neste caso admitimos que as fendas eram muito estreitas de modo que foi possível considerá-las fontes lineares de ondas esféricas que, nos nossos diagramas bidimensionais, aparecem como fontes puntiformes. Dessa forma, pudemos admitir que a intensidade da luz que passa por uma fenda isolada era sempre a mesma (Io) em qualquer ponto P do antepara. Quando a fenda não for estreita, a intensidade da luz em um anteparo distante da fenda não é independente do ângulo q mas diminui quando o ângulo q aumenta. Vamos considerar uma fenda com a largura a. A Fig.16.2 mostra a distribuição de intensidade sobre um anteparo bastante afastado da fenda de largura a, em função do ângulo q . Podemos ver que a intensidade é máxima na direção vertical, sen(q ) = 0 e diminui até zero em ângulo que depende da largura a da fenda e do comprimento de onda l . A maior parte da intensidade da luz está concentrada em uma região central bastante larga, embora existam máximos secundários nos dois lados do máximo central.
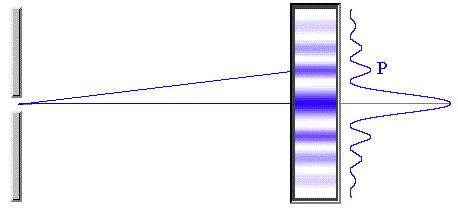
Fig16.2 Distribuição de intensidade
sobre um anteparo bastante afastado
Veja simulação
Usando a regra vetorial podemos calcular o campo elétrico resultante no ponto P. Assim, da Fig.16.3a tiramos que;
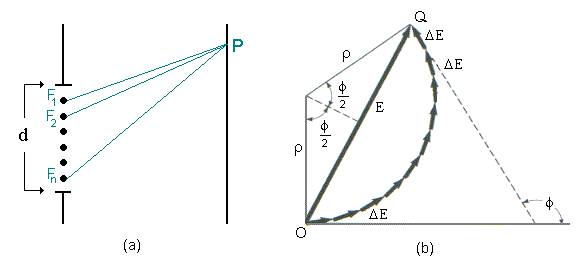
Fig.16.3
O arco OQ, na figura 16.3b é igual a
Combinando as duas equações acima calculamos o campo e resultante, como
A intensidade luminosa no ponto P, pode ser calculada por,
onde b é abertura da fenda. A equação para I está
representada graficamente na figura 16.2
16.3- Difração por N-fendas ou Rede de Difração
Na seção anterior, discutimos a interferência devido a uma fenda não estreita. Faremos a seguir uma generalização deste problema para o caso de n-fendas não estreitas em paralelo. A Fig.4 mostra uma representação esquemática deste caso.
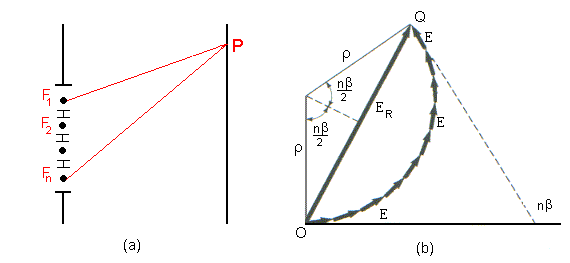
Fig16.4
Assumimos que as fontes são idênticas e emitem ondas eletromagnéticas em fase. O campo elétrico resultante, no ponto P da Fig.4 , é a soma dos campos produzidos por cada fenda. Isto é,
Onde cada Ei é exatamente o campo resultante para uma fenda não estreita, como calculado na seção anterior.
:
:
Usando a regra vetorial, para soma-los, encontramos que,
Substituindo a segunda equação na primeira temos que,
Assim,
Dessa forma a intensidade luminosa assume a forma.
Sendo a a distância entre as fendas e b a largura de cada fenda.
Na simulação abaixo, podemos ver a influência do comprimento de onda e da abertura da fenda no processo de interferência por difração produzido por uma fenda única. Observe que no caso de fenda única a intensidade (I) depende tanto da abertura da fenda (b) quanto do comprimento de onda da luz incidente (l). Neste caso a equação para a intensidade (I) é igual a;
Interferência
por Difração (fenda única)
Modo
de usar: Com o botão esquerdo do mouse você pode variar
o
comprimento de onda (variando as cores), assim como modificar a abertura
da fenda
© Copyright 1997, Sergey
Kiselev and Tanya Yanovsky-Kiselev
Last modified: June 20, 1997
|
|
![]()
O conteúdo desta página
está em constante atualização.
Sugestões serão bem vindas.
![]() Electronic
Address : kcmundim@unb.br
or spedrosa@fis.ufba.br
Electronic
Address : kcmundim@unb.br
or spedrosa@fis.ufba.br
Last Updated: Dez/12/98
Copyright 1997: Kleber C. Mundim.
All rights reserved.
Register No 169.766 - Biblioteca Nacional - Ministério
da Cultura