Aula-2

Aula -2
A Luz como um Fenômeno Eletromagnético

1- A luz e o Eletromagnetismo

Por centenas de anos filósofos e cientistas questionaram sobre a natureza da luz. Isaac Newton (1642-1727) acreditava que a luz consistia de um feixe de partículas, enquanto o físico holandês Christian Huygens (1629-1695) assumia que a luz era um tipo de movimento ondulatório. A disputa sobre a natureza e comportamento da luz foi aparentemente resolvido pelos trabalhos do físico James Clerk Maxwell (1831-1879). Maxwell mostrou que todas as propriedades conhecidas da luz poderia ser explicadas através de quatro equações, conhecidas como as equações de Maxwell. Ele baseou-se na hipótese de que a luz visível, assim com outras formas de radiação, tal como a luz ultravioleta e as ondas de rádios são ondas formadas por campos elétrico e magnético, denominada ondas eletromagnéticas, que se propagam no espaço.

Isaac Newton (1642-1727)

Christian Huygens (1629-1695)

James C.Maxwell (1831-1879)

Uma onda eletromagnética consiste de campos elétrico () e magnético () que oscilam em direções perpendiculares um ao outro e que a direção de propagação desta onda é perpendicular aos campos e , veja Fig.1, por isto estas ondas são denominadas transversais.

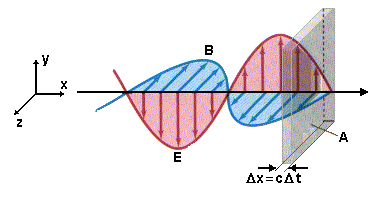
Fig.1a - Propagação de uma onda eletromagnética de acordo com Maxwell

A simulação abaixo representa a propagação de uma onda eletromagnética
na direção Z. Veja que os campos E e B são sempre ortogonais.

Fig.1b - Propagação de uma onda eletromagnética

Para mais detalhes sobre as equações de Maxwell e as demonstrações matemáticas veja Apêndice-1.

Todas as ondas podem ser descritas em termos de suas velocidade, freqüência, comprimento de onda e amplitude como ilustrado na figura Fig.2. O comprimento de onda l (letra grega lambda) é a distância entre dois máximos ou mínimos sucessivos. Conseqüentemente l tem unidade de comprimento. A freqüência n (letra grega nu) é o número de cristas de ondas que passam em um dado ponto de referência por unidade de tempo. A unidade de freqüência é igual ao inverso da unidade de tempo. Freqüentemente usa-se a unidade denominada hertz (Hz), 1Hz = 1 s^-1. A freqüência de 10 Hz significa que 10 cristas da onda passam por segundo em um dado ponto de referência. Se existem n ondas por segundo passando por um ponto, e se o comprimento de onda de cada onda é l , a distância viajada pela onda em 1 segundo é igual ao produto ln , o que corresponde a sua velocidade de propagação, isto é

A luz e todos os outros tipos de radiação eletromagnética têm velocidade de propagação constante que é igual a c = 2,9979246 x 10⁸ m/s, no vácuo. Este resultado pode ser mostrado a partir das equações de Maxwell, veja Apêndice-1.

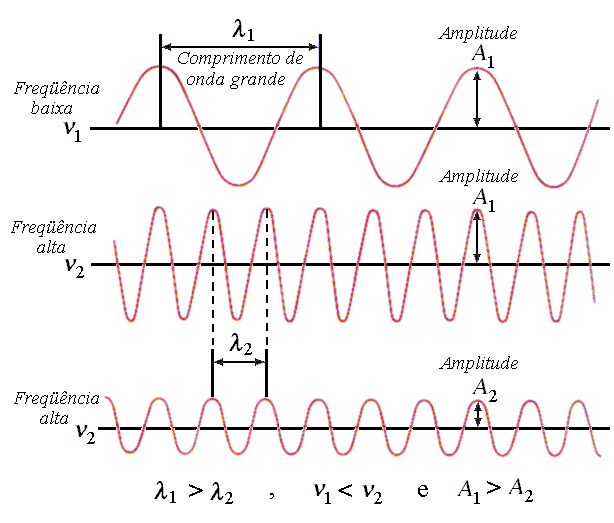
Fig.2 - Propriedades das ondas

Para muitos propósitos, neste curso, será suficientemente acurado usar um valor arredondado para a velocidade da luz com três algoritmos significativos, isto é,

Pode-se mostrar também, através das equações de Maxwell, que qualquer radiação eletromagnética transporta energia. Por exemplo, a energia produzida pelo sol chega a Terra como radiação eletromagnética do tipo ultravioleta, visível e infravermelho. Esta energia é freqüentemente usada por diferentes espécies de seres vivos, transformando-a em diferentes outros tipos de energia, como por exemplo o calor e som.

A amplitude, A, de uma onda é a altura de uma crista de onda. Pode-se mostrar, também que a energia por unidade de volume armazenada em uma onda é proporcional ao quadrado da amplitude (A²). Neste caso a intensidade luminosa, ou brilho da luz, é proporcional a A².

2-Equações de Maxwell

Um dos resultados mais importantes advindo da formulação de Maxwell para o eletromagnetismo é a existência de ondas eletromagnéticas, ou campos elétricos e magnéticos que se propagam no espaço e no tempo. Pode-se mostrar que as equações de Maxwell, tabela 1.1, são suficientes para descrever este fenômeno. Com isto, pode-se concluir que os campos elétrico e magnético se propagam no espaço com velocidade constante e independente do referencial.

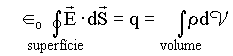		Lei de Gauss Eletrostática
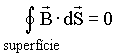		Lei de Gauss Magnetostática
		Lei de Faraday
		Lei de Ampère

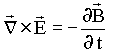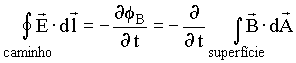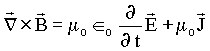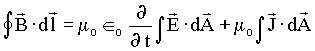Tabela 1.1 - As equações de Maxwell na forma integral e diferencial

Destas equações podemos concluir que ;

   Os campos elétricos criados por cargas elétricas são divergentes ou convergentes.
   Os campos magnéticos são rotacionais, isto é, não existem monopolos magnéticos.
   Campos magnéticos variáveis no tempo geram campos elétricos rotacionais.
   Campos elétricos variáveis no tempo geram campos magnéticos rotacionais.
   Correntes elétricas ou cargas em movimento geram campos magnéticos.

3- A Equação de Onda Eletromagnética e sua Velocidade

Das equações de Maxwell, apresentadas na Tabela 1.1, pode-se deduzir um conjunto de equações que descrevem a propagação das ondas eletromagnéticas, isto é, a propagação dos campos elétricos e magnéticos, as quais têm a seguinte forma.

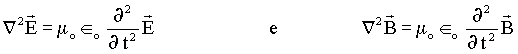
Os estudantes mais interessados neste tema, podem encontrar no Apêndice, uma discussão mais detalhada desta teoria, assim como as demonstrações matemáticas aqui citadas. Para isto, "click" com o "mouse" na palavra apêndice, acima.

No caso geral, as soluções destas equações são complexas pois temos que resolver, simultaneamente, um sistema de seis equações diferenciais de segunda ordem, no espaço e tempo. Estas equações têm soluções simples quando tratamos uma onda se propagando no vácuo. Neste caso, os campos elétricos e magnéticos, que são soluções das equações de onda têm a seguinte forma;

onde k = 2p /l e w = 2p n . k é referido como número de onda; l - comprimento da onda eletromagnética; n - freqüência e w é a freqüência angular.

Fig.- Propagação de uma onda eletromagnética

Observe nesta simulação que os campos elétrico e magnéticos são perpendiculares entre si. Das equações acima pode-se mostrar que a velocidade de propagação da onda é igual a

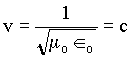
onde e são, respectivamente, as permitividades magnética e elétrica no vácuo.

Destas análises, pode-se concluir que os campos elétrico e magnético se propagam no espaço com velocidade constante e independente do referencial.

Nos anos que precederam a unificação da teoria de Maxwell, os físicos consideravam que a teoria da luz não estava relacionada à teoria da eletricidade e magnetismo. Maxwell mostrou com sua teoria unificada, não só o comportamento ondulatório do eletromagnetismo como também que as ondas eletromagnéticas são geradas sempre que cargas elétrica são aceleradas. Portanto, ele foi capaz de explicar o fato de que as ondas eletromagnéticas seriam radiadas por qualquer circuito no qual correntes alternadas fluem. Esses resultados foram confirmados através do primeiro transmissor-receptor de rádio, construído por Hertz - em 1887, logo após a morte de Maxwell.

As ondas eletromagnéticas geradas por campos, da forma demonstrada nas equações acima, são denominadas ondas planas. Como os campos E e B são transversais à direção de propagação da onda, elas devem ser do tipo transversais. Neste aspecto, elas são análogas às ondas geradas em uma corda de instrumento musical. As ondas geradas por E e B, neste caso, são do tipo linearmente polarizadas e monocromáticas (w = 2pn fixa), mas em geral as ondas eletromagnéticas são não planas, não são polarizadas e nem policromáticas.

A teoria envolvida na descrição do transporte de energia em ondas eletromagnéticas pode ser encontrada no Apêndice-2.

4- Aplicação (velocidades clássica e relativística)

No exemplo a seguir faremos comparações entre a velocidade da luz e as velocidades de objetos que convivemos diariamente. Isto será feito comparando as velocidades obtidas pelas Mecânicas Clássica e Relativística.

Inicialmente, estudaremos dois objetos viajando em sentidos opostos, à uma velocidade de v₁ = v₂ = 50.000 km/h com relação a uma dado observador fixo. Neste caso, apesar de v ser muito grande quando comparada com as velocidades comuns ao nosso dia a dia, ela é ainda muito pequena comparada com a velocidade da luz, isto é v₁ << c. De acordo com as Mecânicas Clássica e Relativística, as velocidades relativas para os dois foguetes são iguais a;

Mecânica Clássica

Mecânica Relativística

Estes resultados leva-nos a concluir que, para velocidades pequenas comparadas com a velocidade da luz, as Teorias Clássica e Relativística fornecem resultados semelhantes. Isto significa que, neste caso, a teoria clássica ou Newtoniana é suficiente para descrever o fenômeno em questão.

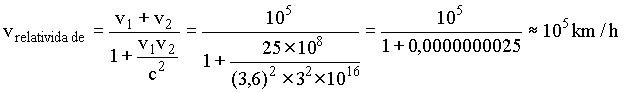
Suponhamos agora, que os nossos dois objetos sejam duas partículas criadas com a fragmentação de um núcleo de urânio. Assumimos, por hipótese, que estas partículas criadas saem, em sentidos opostos, com velocidades da ordem de 60% da velocidade da luz, isto é v₁= v₂ = 0,6c. Usando estas informações as velocidades previstas pelas duas teorias são, respectivamente,

Mecânica Clássica

Mecânica Relativística

Neste caso as duas teorias fornecem resultados completamente divergentes. O que mostra que a Teoria Clássica e Teoria da Relatividade não concordam-se o que mostra que teoria clássica ou Newtoniana começa a falhar.

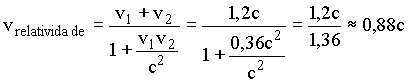
Apêndices
Selecione com o "mouse" o item que lhe interessa.

- Apêndice 1 : Demonstrações
                             - As equações de Maxwell na forma diferencial
                             - A equação de uma onda eletromagnética
                             - A velocidade de uma onda eletromagnética

- Apêndice 2 : Transporte de Energia em Ondas Eletromagnéticas

- Apêndice 3 : Interferência e Difração de Ondas Esféricas

O conteúdo desta página está em constante atualização.
Correções no texto e sugestões serão bem vindas.