Equação de Schrödinger para Sistemas Atômicos Esfericamente Simétricos
Átomos Hidrogenoides
A energia potencial de uma partícula de massa m, a qual se move em um campo de força central esfericamente simétrico, depende somente da distância r entre a partícula e o centro da força. A equação de Schrödinger para um destes sistemas é igual a;
Como o sistema tem simetria esférica, a equação diferencial acima fica mais simples de ser resolvida se for escrita num sistema de coordenadas que seja apropriada à simetria do problema, que neste caso é esférica. Veja mais detalhes no Anexo. Assim, devemos escrever o operador Laplaciano e conseqüentemente a equação de Schrödinger em coordenadas esféricas, isto é,
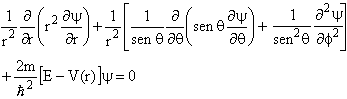 (2)
(2)Os estados energéticos deste sistema são determinados resolvendo esta equação diferencial, cujas soluções são continuas, têm derivadas contínuas em r,
na qual a parte radial R(r) é independente das componentes angulares, e a parte angular Y(q,f) é independente da componente radial r. Substituindo a eq.(3) em (2) tem-se que;
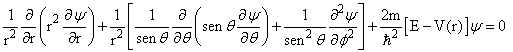
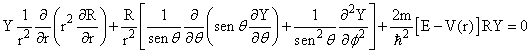 (4)
(4)Multiplicando ambos lados de eq.(4) por r2/RY e re-agrupando os termos dependentes nas partes radial e angular, separadamente, obtém-se;
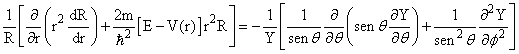 (5)
(5)Nesta equação, observamos que o lado esquerdo depende apenas, por hipótese, da coordenada r, enquanto lado direito não depende de r. Conseqüentemente, esta equação pode ser identicamente satisfeita somente se ambos termos, lado direito e lado esquerdo, são uma constante C, isto é;
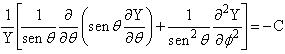 (7)
(7)De onde tiramos que a energia total E é determinada pela equação radial (eq.6). Já a eq.(7) é independente da energia E e da energia potencial V(r).
Na equação (7), de forma semelhante ao caso anterior, também pode ser aplicado o método de separação de variáveis em Y, isto é;
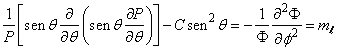 (9)
(9)para a qual
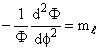 (10)
(10)já foi resolvida anteriormente, cuja solução é da forma;
O lado esquerdo da equação (9) pode ser re-escrita por,
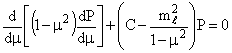 (11)
(11)onde
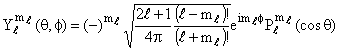 (12)
(12)
A função ![]() pode ser computada a partir dos polinômios de Legendre, como
a seguir;
pode ser computada a partir dos polinômios de Legendre, como
a seguir;
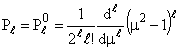 ,
(13)
,
(13)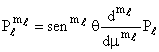 (14)
(14)|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As funções ![]() são denominadas por harmônicos esféricos e formam um
conjunto completo de funções orto-normais, isto é;
são denominadas por harmônicos esféricos e formam um
conjunto completo de funções orto-normais, isto é;
Os três números quânticos para
o caso dos sistemas aqui estudados devem satisfazer as seguintes relações;
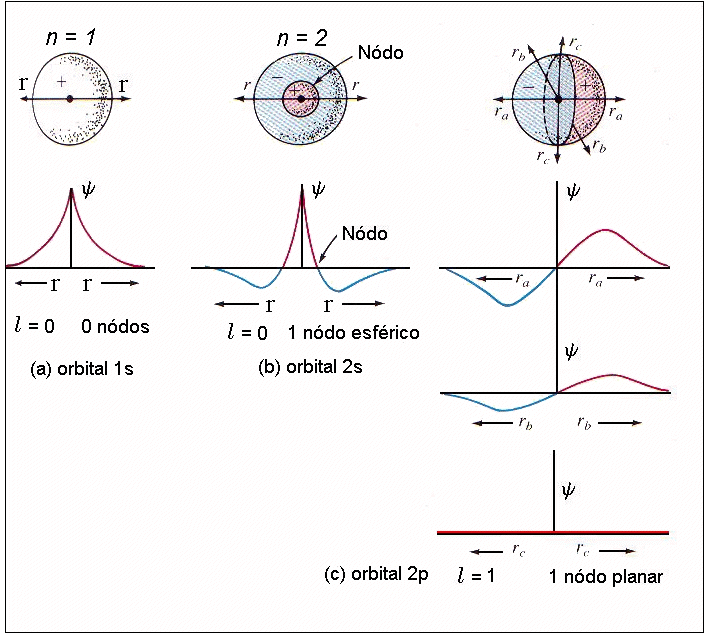
Fig.1 Superfície Nodal
O número de nós N é dado pela relação N = n-1, por exemplo no caso n = 2 temos apenas 1 nó que é na forma esférica para orbital 2s e planar para o orbital 2p, como mostra a figura acima.
Estes resultados são equivalentes à aqueles obtidos na teoria ondulatória em superfícies, como mostra a figura abaixo. As ondas provocadas na superfície de um tambor são descritas por equações matemáticas e soluções semelhantes a aquelas obtidas na mecânica quântica.
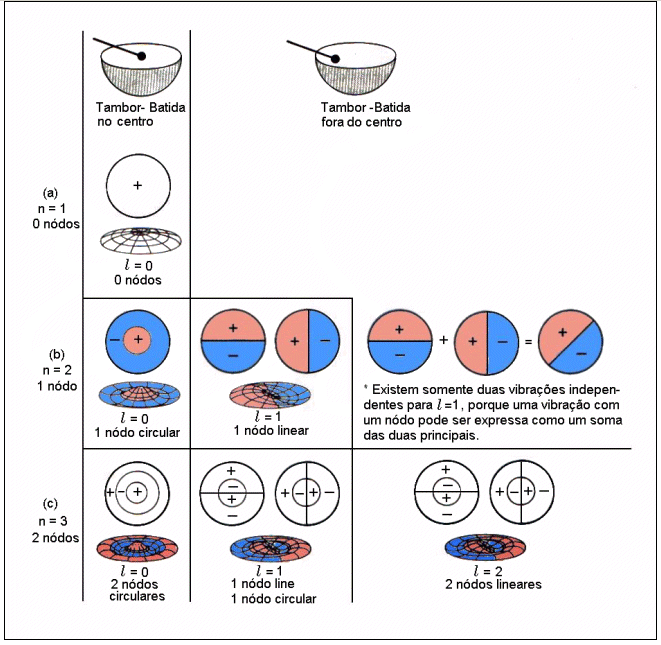
Fig.2 Superfície Nodal
Soluções Esféricas e não Esféricas para Átomos Hidrogenoides
|
|
|
|
|
|
1 |
0 |
0 |
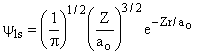 |
|
2 |
0 |
0 |
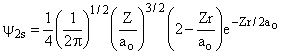 |
|
3 |
0 |
0 |
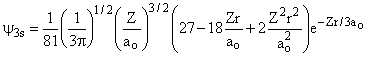 |
|
|
|||
|
2 |
1 |
±1 |
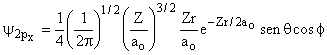 |
|
2 |
1 |
±1 |
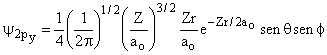 |
|
2 |
1 |
0 |
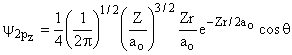 |
|
|
|||
|
3 |
1 |
±1 |
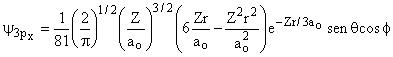 |
|
3 |
1 |
±1 |
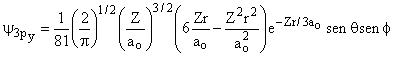 |
|
3 |
1 |
0 |
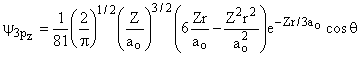 |
|
|
|||
|
3 |
2 |
0 |
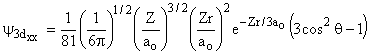 |
|
3 |
2 |
±1 |
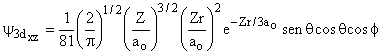 |
|
3 |
2 |
±1 |
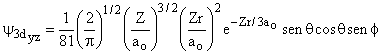 |
|
3 |
2 |
±2 |
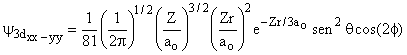 |
|
3 |
2 |
±2 |
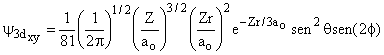 |