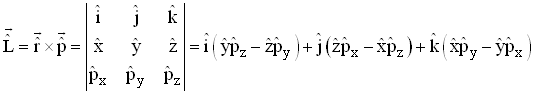Operador Momento Angular Orbital

O operador momento angular orbital pode ser expresso em coordenadas Cartesianas pela relação

                            (1)

ou mais ainda,

,     .                                (2)

Freqüentemente é mais conveniente trabalhar com este operador em coordenadas esféricas r, q, f; as quais estão correlacionadas com as coordenadas cartesianas pelas relações de transformação,

                                                  (3)

cujas relações podem ser facilmente obtidas da figura abaixo,

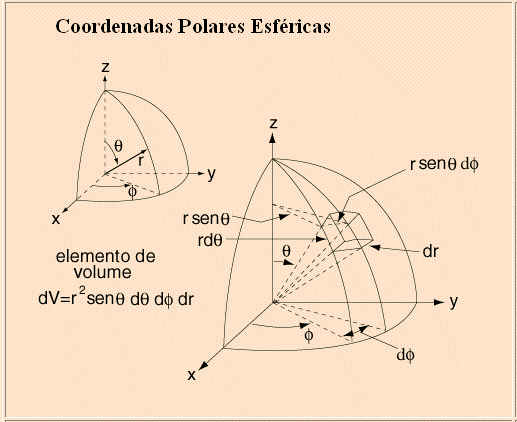
Assim, notamos que cada coordenada Cartesiana  x, y, e z é uma função das coordenadas esféricas e cada coordenada esférica r, q, f. é consequentemente uma função das coordenadas Cartesianas. A partir das relações contidas na equação (3), podemos determinar as relações que conectam os operadores derivadas em ambos sistemas de coordenadas como a seguir,

                                                                       (4a)

                                                                      (4b)

.                                                                         (4c)

As três equações acima podem ser escritas em termos de produto de matrizes, isto é;

                                                                                                      (4d)

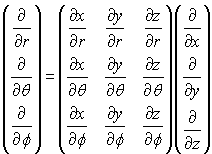                                                                         (4e)

Onde, M é a matriz que transforma coordenadas cartesianas em esféricas. Caso necessite de transformar coordenadas esféricas em cartesianas basta encontrar a matriz inversa de M e multiplicá-la em ambos lados da equação 4(d).

        Substituindo as expressões (3) na equação (4e) e resolvendo as respectivas derivadas encontramos a matriz que faz a transformação de coordenadas Cartesianas em polares esféricas, como é mostrado a seguir,

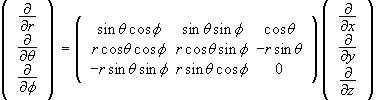.                                                (5)

Invertendo a matriz do lado direito da equação (5) encontramos a matriz que faz a operação inversa, isto é transforma coordenadas esféricas em Cartesianas, como a seguir,

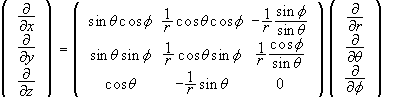.                                            (6)

Fazendo uso destes resultados podemos escrever, agora, o operador momento angular orbital em coordenadas esféricas. Isto é, a componente x é dada por,

                     (7)

Procedendo de forma similar, podemos encontrar suas coordenadas y e z, isto é,

.

Em resumo temos que,

Operador momento Angular	Coordenadas Cartesianas	Coordenadas Esféricas

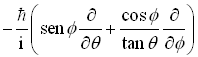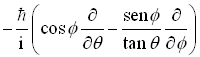Lembramos que o operador momento angular também pode ser determinado pela relação  L²=L_x²+L_y²+L_z²,

.                            (8)

L₊=L_x+iL_y,      e        L_-=L_x-iL_y,                                                                                                                (9)

.                                                              (10)

Usando um procedimento análogo pode-se mostrar que o operador Hamiltoniano tem a seguinte forma em coordenadas esféricas,

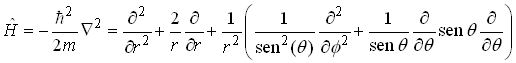                                          (11)