Aula-14

Aula 14

Movimento Circular e o Momentum Angular Orbital

Consideremos o caso de uma partícula de massa m se movendo no plano XY. A energia (E) total dessa partícula é a própria energia cinética, desde que ela não esteja sobre a influência de potencial externo variável, isto é V = 0. Assim a energia é igual a;

(1)

De acordo com a mecânica clássica (newtoniana) o momento angular sobre a partícula é definido por;

(2)

Para o caso em que uma partícula de massa m tenha um movimento restrito ao plano XY, o momento angular deve ter apenas a componente na direção do eixo Z, como mostra a Fig.1. Então neste caso tem-se que,

(3)

A energia E pode ser expressa em função de L, da seguinte forma

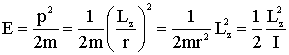(4)

Onde é o momento de inércia da partícula.

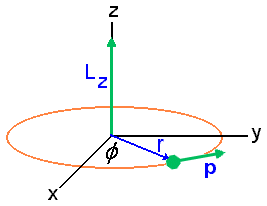
Fig.1

Veja no endereço anexo as demonstrações que levam os operadores em coordenadas Cartesianas em Esféricas. ANEXO

Mostraremos a seguir que o momento angular desta partícula não pode assumir qualquer valor, mas sim apenas valores discretos e, portanto ele é uma grandeza quantizada.

O operador Hamiltoniano para uma partícula em movimento no plano é igual a;

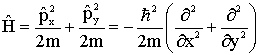(5)

Lembrando ainda que o operador momentum é expresso na forma diferencial, isto é:

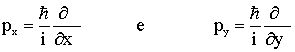(6)

a equação de Schrödinger pode ser escrita da seguinte forma;

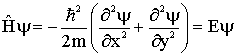(7)

Vimos anteriormente que a energia E está associada ao movimento rotacional e conseqüentemente deve ser uma função do ângulo azimutal f, veja Fig.1. Neste sentido será conveniente escrever o operador H em um sistema de coordenadas onde a variável angular f aparece explicitamente. Como a rotação ocorre num plano XY então, o sistema de coordenadas apropriado é o de coordenadas polares, isto é;

(8)

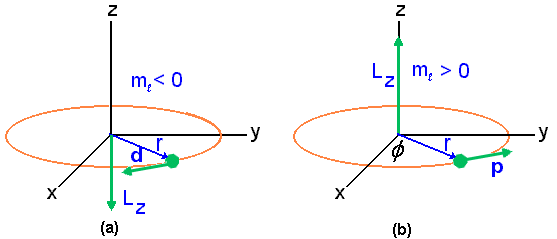
Fig.2

Usando as relações acima que conectam as coordenadas cartesianas e polares, podemos escrever o operador Hamiltoniano neste sistema de coordenadas da seguinte forma;

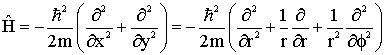(9)

Como o raio r é fixo (constante), não haverá taxa de variação da energia em função de r. Conseqüentemente, as derivadas em r devem ser descartadas. Assim, temos que;

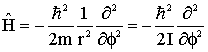(10)

Conseqüentemente, a equação de Schrödinger pode ser rescrita da seguinte forma;

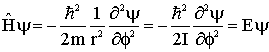(11)

o que implica em,

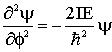(12)

cuja solução é da seguinte forma;

(13)

Sendo esta função (eq.13) uma solução da equação de Schrödinger ela deve satisfazer a igualdade estabelecida na eq.12. Assim, temos que;

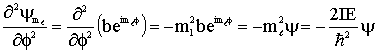(14)

de onde tiramos que;

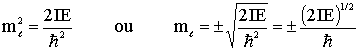(15)

Substituindo este resultado na equação (13) tem se que a função de onda pode ser reescrita por;

(16)

Para que a função de onda seja de quadrado somável (postulado IV da Mecânica Quântica), isto é normalizável, ela deve satisfazer a relação;

(17)

(18)

De onde tiramos o valor de . Substituindo este resultado na função de onda (eq.16), tem-se;

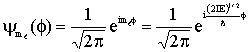(19)

Observe que a função dada na equação (19) é cíclica, isto é;

(20)

o que pode ser verificado por;

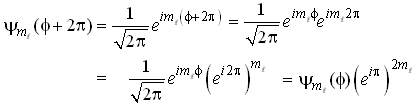(21)

mas , conseqüentemente, tem se que;

(22)

Para que a condição (eq.21) seja satisfeita é necessário que , de onde tiramos que m_l deve ser um número inteiro positivo ou negativo, isto é;

(23)

O Operador Momento Angular

Sabemos da mecânica clássica que o operador momento angular é definido como o produto vetorial entre o vetor posição (r) e o vetor momento linear (p);

caso clássico (24)

Por definição de produto vetorial, em álgebra, tem-se que;

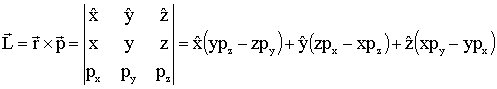(25)

(26)

No caso de uma partícula se movendo no plano XY e para V=0, apenas a componente Z do momento angular é diferente de zero, isto é;

caso clássico (27)

Podemos encontrar o corresponde quântico do momento angular da seguinte forma;

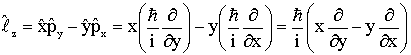(28)

que é a componente Z do operador momento angular orbital, quântico, expressa em coordenadas cartesianas. Usando as equações (8) podemos escrevê-lo em coordenadas polares como a seguir;

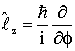(29)

Veja no endereço anexo as demonstrações que levam os operadores em coordenadas Cartesianas em esféricas. ANEXO

Autovalor do Operador Momento Angular

O autovalor do operador momento angular pode ser calculado da seguinte forma,

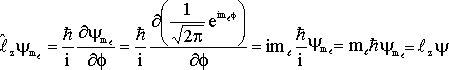(30)

Assim o autovalor do operador momento angular é igual a;

onde (31)

Rotações em 3 Dimensões

Para o caso tri-dimensional o operador Hamiltoniano assume a forma;

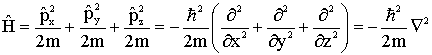(32)

e a equação de Schrödinger;

(32a)

No caso tridimensional tem-se dois tipos de rotações independentes, são elas a azimutal (f) e latitudinal (q). Como o movimento nas duas direções são independentes a função de onda pode ser escrita como um produto de duas funções e , como a seguir;

(33)

Neste sentido, seria conveniente expressar o operador Laplaciano em coordenadas esféricas, como a seguir;

(34)

onde

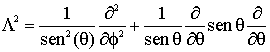(35)

No caso em que r é fixo (constante) tem-se que;

(36)

Com este resultado podemos escrever a equação de Schrödinger em coordenadas esféricas como a seguir;

(37)

(38)

onde e .

Dividindo ambos lados da equação acima por e multiplicando por , temos que

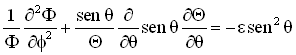(39)

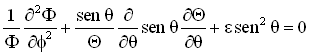(40)

Observando a equação acima notamos que o primeiro termo depende apenas da coordenada azimutal e os outros termos dependem apenas da coordenada latitudinal . Isto leva-nos as seguintes relações;

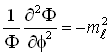(41)

(42)

A solução da segunda equação (Eq. 42) pode ser obtida em termos das funções de Legendre, como veremos nas próximas seções.

Voltar à página principal

Voltar ao início desta página

O conteúdo desta página está em constante atualização.
Correções no texto e sugestões serão bem vindas.

Electronic Address : kcmundin@unb.br
Last Updated: Jul/17/2002
Copyright 1997: Kleber C. Mundim. All rights reserved.
Register N^o 169.766 - Biblioteca Nacional - Ministério da Cultura
phone: 55 61 307 2150