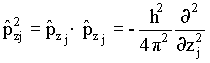Aula 8
Introdução a Mecânica Quântica
![]() 1. Insuficiência da Física
Clássica
1. Insuficiência da Física
Clássica
A aplicação da Mecânica e da Eletrodinâmica clássica aos edifícios atômicos e moleculares conduz rapidamente a conclusões insustentáveis, em total desacordo com a experiência. Assim, se as leis clássicas se aplicassem à um elétron gravitando em torno de um núcleo positivo, ele deveria irradiar continuamente ondas eletromagnéticas, em conseqüência, perderia energia até finalmente cair sobre o núcleo. Como sabemos, neste modelo tal como se encontra no átomo de hidrogênio, por exemplo, é estável e não irradia energia. Da mesma maneira é absolutamente impossível explicar a existência de moléculas a partir da Física Clássica.
Esta situação foi o motivo de diversas tentativas no sentido de resolver as dificuldades encontradas. A teoria de Bohr para o átomo de hidrogênio (1910) é um exemplo de uma destas tentativas. Entretanto, como todas as teorias foram formuladas segundo os princípios da Física Clássica e sem possibilidade de generalização elas fracassaram completamente. Seria necessário repensar, então, toda a Física corpuscular.

Niels Bohr
Foi o trabalho de Louis de Broglie que em 1924 lançou as bases de uma nova mecânica chamada ondulatória ou quântica (os dois qualificativos são sinônimos neste caso). Completada pelos trabalhos de Heisenberg, Schrödinger, Pauli, Dirac e outros mais, a Mecânica Ondulatória forma, em nossos dias, um conjunto coerente e apropriado ao tratamento de sistemas corpusculares necessitando, entretanto, de uma bagagem matemática considerável.
Em 1924, Louis de Broglie,
lembrando-se da natureza dualística dos fótons (sugerida por Einstein ao
estudar o efeito
fotoelétrico), e considerando que todos os fenômenos naturais envolviam certa
forma de matéria e de radiação (ondas
eletromagnéticas), sugeriu que assim como "as ondas de luz" tinham
propriedades de partículas o inverso também deveria
ser válido, isto é:
|
"A toda partícula com momento linear p estaria associada uma onda de comprimento l, isto é : l= h/p, onde h é a constante de Planck e p o momento linear da partícula. Esta relação implicaria que todos os corpos massivos ou partículas, tais como uma bola de bilhar e um elétron, teriam também propriedades de ondas, cujas características seriam regidas pela mesma teoria das radiações. " |

L. de Broglie
O comprimento de onda de De Broglie (l = h/p) foi escolhido de tal modo que a órbita de raio r contivesse um número inteiro n de ondas de matéria, ou seja,
De onde tiramos a quantização do momento angular, previamente postulado por Bohr,
A natureza dualística
da matéria era, então, sugestiva. A existência de ondas de matéria sugeria a
possibilidade de se construir uma equação de onda que explicasse naturalmente o
comportamento dos elétrons, átomos e moléculas. Neste sentido, em 1925, W.
Heisenberg desenvolveu uma nova teoria quântica baseada no princípio da
correspondência sugerido por Bohr. Heisenberg formulou sua teoria utilizando-se
do cálculo matricial. Ironicamente, essa teoria escapou à atenção de muitos
pesquisadores, devido a sua formulação matemática aparentemente complexa.
Em 1926, quase ao mesmo tempo, E.
Schroedinger publicou as suas idéias propondo uma nova teoria quântica.
Formuladas de forma diferentes essas duas teorias são no entanto, idênticas
quanto aos seus resultados. Hoje, quase dois séculos depois, essas teorias
ainda constituem o esteio dos conceitos modernos da estrutura da matéria.
Schroedinger, diferentemente de
Heisenberg, foi levado a formular uma nova mecânica dentro da teoria
ondulatória, a qual já era bem estabelecida. Ele tomou como base a equação de
onda de d´Alembert que rege o movimento dos sistemas ondulatório no espaço e no
tempo, a qual tem a forma:
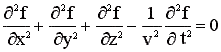
Levando em conta que as partículas, como por exemplo o
elétron, se comportam como ondas, então seria de se esperar que a equação de
d'Alembert também se aplicasse à descrição dos movimentos eletrônicos no átomo.
![]() 2. Princípios Gerais da
Mecânica Quântica
2. Princípios Gerais da
Mecânica Quântica
A Mecânica Clássica permite
determinar a evolução de um sistema ao longo do tempo quando se conhece as
condições iniciais e as forças agindo sobre o sistema. Em particular, pode-se
prever, para cada elemento que constitui o sistema, a trajetória e a lei do
movimento sobre esta trajetória. No caso da mecânica Newtoniana a cada
instante, nós conhecemos a posição e a velocidade de cada partícula. Podemos
então dizer que uma tal mecânica é determinista e muito ambiciosa. No universo
microscópio das partículas, de acordo com o princípio da incerteza de
Heizenberg, é impossível descrever perfeitamente o estado de um sistema, como
por exemplo a posição e velocidade de um elétron no interior do átomo,
simultaneamente.
Tudo que nós podemos conhecer sobre o
movimento de um sistema de partículas se reduz a uma função complexa Y dependente das coordenadas (x1,
x2,..xN) das partículas e do tempo t. Esta função é
chamada função de onda, advindo daí o qualificativo ondulatório dado a esta
mecânica. De acordo com Max Born, esta função de onda não possui um significado
físico, mas sim o quadrado de seu módulo:
![]() 1
1
(Y* = imaginário conjugado
de Y ), representa a probabilidade de
encontrar, no instante t as diversas partículas constituindo o sistema nos
pontos de coordenadas x1, x2,...xN. Em outros
palavras podemos dizer que a probabilidade de encontrar o sistema no instante t
em um volume V do espaço (x1, x2,...xN) é dado
por,
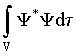 ,
2
,
2
a integração sendo realizada sobre todas as coordenadas. Se o volume V é infinito, este volume contém certamente o sistema, então
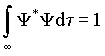 .
3
.
3
Esta condição fundamental chamada de condição de normalização da função de onda exige que a função Y seja de quadrado somável e em particular que ela seja zero no infinito.
Na concepção clássica, uma
partícula se encontra ou não, em um determinado instante, em um dado ponto do
espaço. Pela Mecânica Quântica nós só podemos conhecer a probabilidade de
encontrar a partícula no ponto considerado. O que leva a dizer que se
repetirmos estas medidas simultaneamente sobre um número grande de sistemas
idênticos e independentes (átomos em um gás diluído, por exemplo),
![]() representa a densidade de presença da partícula. Tudo se
passa então - a nossa escala - como se as partículas tivessem perdido sua
individualidade e fossem substituídas por uma nuvem contínua de densidade igual
ao quadrado do módulo da função de onda correspondente. Desta maneira, à cada
partícula se encontra associada uma função de onda, resumindo assim, tudo o que
é possível saber sobre ela.
representa a densidade de presença da partícula. Tudo se
passa então - a nossa escala - como se as partículas tivessem perdido sua
individualidade e fossem substituídas por uma nuvem contínua de densidade igual
ao quadrado do módulo da função de onda correspondente. Desta maneira, à cada
partícula se encontra associada uma função de onda, resumindo assim, tudo o que
é possível saber sobre ela.
O problema maior desta teoria é a determinação desta função de onda. Schrödinger (1926) mostrou que ela era solução de uma equação em derivadas parciais de segunda ordem, onde ele forneceu igualmente suas regras de construção. Será indicado em seguida os pontos essenciais relativos à construção desta equação e à estrutura das funções de onda.

E. Schrödinger
Para um sistema isolado, a função de onda pode ser separada da seguinte forma:
![]() 4
4
onde os termos ![]() e
e ![]() são os fatores espacial e
temporal.
são os fatores espacial e
temporal.
Nesta equação E é a energia total do sistema, a qual é constante, visto que o sistema é isolado, h é a constante de Planck (6,6 x 10-27 c.g.s) e i é a parte imaginária. Y (x1, x2,...xN) é uma função de onda comportando apenas as variáveis espaciais. Esta função satisfaz a equação chamada de Equação de Schrödinger que pode ser escrita simbolicamente por:
![]() ,
5
,
5
H é designado um operador diferencial que transforma Y . Se multiplicarmos esta equação à esquerda por Y* e integrá-la em relação às
variáveis espaciais, obteremos
![]() 6
6
visto que Y é normalizada.
Na prática, constrói-se o
operador
![]() , algumas vezes chamado Hamiltoniano, substituindo na
expressão clássica para a energia total de um sistema constituído de N partículas, as quantidades de
movimento px associado as
coordenadas cartesianas x, pelos
operadores diferenciais:
, algumas vezes chamado Hamiltoniano, substituindo na
expressão clássica para a energia total de um sistema constituído de N partículas, as quantidades de
movimento px associado as
coordenadas cartesianas x, pelos
operadores diferenciais:
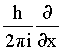 .
7
.
7
Para um sistema de partículas j de
massas respectivas mj, a energia total E é a soma da energia
cinética (T) e a da energia potencial (V). A energia cinética é função das
velocidades que por sua vez pode ser expressa em função das quantidades de
movimento, assim,
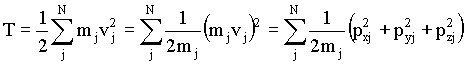 ,
8
,
8
onde pxj , pyj
e pzj são
as componentes do vetor quantidade de movimento da partícula j, isto é,
![]() 9
9
A resolução da equação ![]() fornece a função de
onda em termos do parâmetro E que é a energia total do sistema. Como vimos, a
condição de normalização exige que esta função seja de quadrado somável. O
estudo matemático das soluções da equação de Schrödinger mostra que esta
condição é realizada somente para certos valores discretos de E. Em outros
termos, a energia inicial de um sistema não pode ser arbitrariamente imposta
como na Mecânica Clássica.
fornece a função de
onda em termos do parâmetro E que é a energia total do sistema. Como vimos, a
condição de normalização exige que esta função seja de quadrado somável. O
estudo matemático das soluções da equação de Schrödinger mostra que esta
condição é realizada somente para certos valores discretos de E. Em outros
termos, a energia inicial de um sistema não pode ser arbitrariamente imposta
como na Mecânica Clássica.
As funções Yi de quadrado somável são ditas auto-funções do operador H cujas energias associadas Ei são denominadas de auto-valores deste operador.
Pode-se mostrar igualmente que as funções de onda Yi , soluções da equação de Schroedinger acima, são ortogonais, isto é:
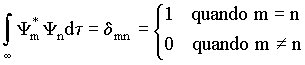 10
10
onde dmn é a delta de Dirac.
O conhecimento da função de onda determina completamente o sistema no ponto de vista da mecânica quântica. Na realidade, as mesmas regras de construção relativas ao operador Hamiltoniano associado à energia se aplicam à uma grandeza qualquer. A expressão clássica desta grandeza corresponde a um operador F; o resultado da medida macroscópica sendo dada por
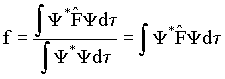 11
11
![]() 3.
Interpretação da Mecânica Ondulatória e seus Postulados
3.
Interpretação da Mecânica Ondulatória e seus Postulados
Schödinger, para introduzir a sua
formulação para a Mecânica Quântica se baseou no modelo da Mecânica Ondulatória
Clássica. A idéia básica era encontrar uma equação equivalente a equação de
Hamilton para a mecânica clássica.
No caso de um sistema de N partículas, por exemplos elétrons,
assume-se que a energia potencial é função somente das coordenadas ![]() :
:
![]() 12
12
Como a energia total do sistema (E) é igual a soma das energias cinética e potencial, temos que,
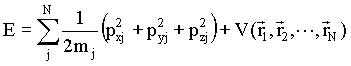 13
13
Na mecânica quântica substituímos as quantidade de movimento
pelos seus operadores correspondentes, como a seguir
|
|
|
|
|
|
Assim temos que
|
|
|
|
|
|
O operador energia equivalente ao clássico (eq.13) pode ser
obtido usando a equação 15, como a seguir
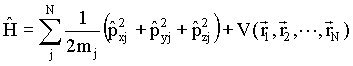 16
16
ou
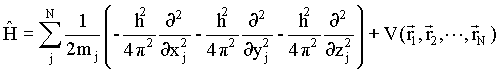 17
17

onde ![]() é o operador Laplaciano relativo à partícula
j, isto é,
é o operador Laplaciano relativo à partícula
j, isto é,
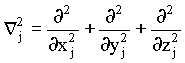 .
18
.
18
Assim a equação de Schrödinger (eq.5) assume a forma
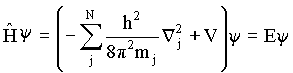 19
19
![]() 4.
O princípio de Mínima Ação e a equação de Schrödinger
4.
O princípio de Mínima Ação e a equação de Schrödinger
Na seção 3, discutimos o princípio de mínima ação ou princípio de Hamilton. Na mecânica clássica, a variação da integral de ação resulta em uma equação diferencial que, uma solucionada, fornece todas as informações do sistema em estudo. Portanto, espera-se que a variação de uma integral equivalente forneça uma equação que descreva completamente o sistema quântico, a qual será denominada de equação de Schrödinger. Desta forma a equação de Schrödinger pode ser deduzida da mesma maneira que a equação de Euler-Lagrange, discutida na seção 3, utilizando para isto o método variacional.
Para formular o problema variacional na mecânica quântica, considere a integral de ação:
![]() 20
20
em que
![]() é o operador Hamiltoniano atuando na função de onda Y.
Esta integral expressa o valor esperado da energia (E). Mas, o problema quântico
está vinculado à normalização da função de onda com apresentado na equação (3).
Portanto, será necessário a utilização do método dos multiplicadores de Lagrange
para se efetuar a variação, já que a equação (3) é uma equação de vínculo ou
condição que a função de onda deve satisfazer. Assim, sabendo que
é o operador Hamiltoniano atuando na função de onda Y.
Esta integral expressa o valor esperado da energia (E). Mas, o problema quântico
está vinculado à normalização da função de onda com apresentado na equação (3).
Portanto, será necessário a utilização do método dos multiplicadores de Lagrange
para se efetuar a variação, já que a equação (3) é uma equação de vínculo ou
condição que a função de onda deve satisfazer. Assim, sabendo que
![]() ,
tem-se
,
tem-se
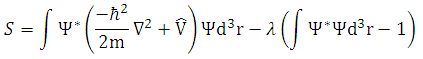 (21)
(21)
ou ainda,
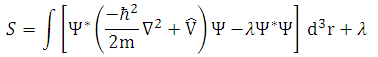 (22)
(22)
em que apenas subtraiu-se zero na equação (20). Aplicando a variação na equação (22), em que l é o multiplicador de Lagrange, tem-se que
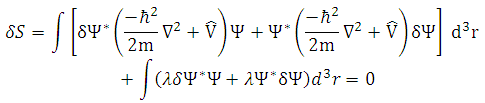 (23)
(23)
Neste caso o multiplicador de Lagrange l é uma constante, assim dl = 0. Re-escrevendo a equação (23) obtemos,
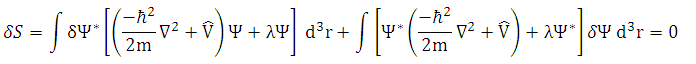 (24)
(24)
As funções de onda Y e Y* variam de forma independente. Desta forma, a condição dS = 0 fornece duas equações diferenciais equivalentes, do tipo,
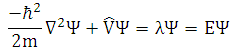 ,
(25)
,
(25)
que é a própria equação de Schrödinger não dependente do tempo.
Em resumo
podemos escrever alguns dos postulados da nova Mecânica como,
i.
A todo sistema corresponde uma função de
onda ![]()
ii. A função de onde deve ser de quadrado integrável e normalizada,
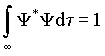
iii.
A seguinte correspondência existe entre as
variáveis dinâmicas e os seguintes operadores:
|
Variáveis Operadores |
|
|
|
|
|
|
|
|
|
|
|
|
![]()
O conteúdo desta página está em
constante atualização.
Correções no texto e sugestões serão bem vindas.
![]() Electronic Address : kcmundin@unb.br
Electronic Address : kcmundin@unb.br
Last Updated: Aug/07/2007
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No 169.766 -
Biblioteca Nacional - Ministério da Cultura
phone: 55 71 237 2033 FAX
55 71 235 5592
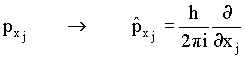
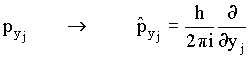 14
14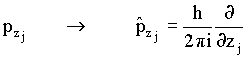
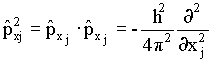
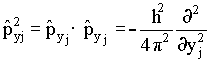 15
15