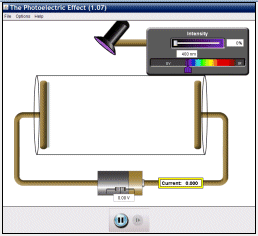
O Efeito Fotoelétrico
O Efeito Compton
Enquanto Planck considerava a
quantização
da energia, na sua teoria da radiação do corpo negro,
como
um artifício de cálculo, Einstein enunciou a audaciosa
hipótese
da quantização da energia ser uma propriedade fundamental
da energia eletromagnética. Três anos mais tarde, aplicou
a idéia da quantização da energia às
energias
moleculares para resolver outro enigma da física- a
discrepância
entre os calores específicos, calculados pelo teorema da
equipartição
da energia, e os calores observados experimentalmente em temperaturas
baixas.
Depois, as idéias da quantização da energia foram
aplicadas às energias atômicas, por Niels Bohr, na
primeira
tentativa de explicar os espectros atômicos. A
hipótese de Einstein sugere que a luz, ao atravessar o
espaço,
não se comporta como uma onda, mas sim com uma partícula.
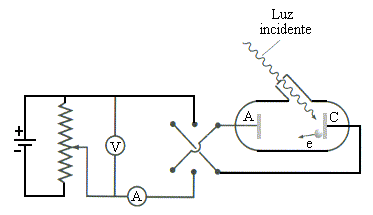 Fig. 1 - Diagrama esquemático do aparelho básico para investigar o efeito fotoelétrico |
|
O efeito fotoelétrico foi descoberto por
Hertz, em 1887, e estudado por Lenard em 1900. A Fig.1 mostra o
diagrama
esquemático do aparelho básico para a
realização do
experimento de investigação do efeito
fotoelétrico. Quando a
luz incide sobre a superfície metálica limpa, no catodo
C,
provoca a emissão de elétrons pela superfície. Se
alguns
destes elétrons atingirem o anodo A, haverá uma corrente
no
circuito externo. O número de elétrons emitidos que
atingem o
anodo, pode ser aumentado ou diminuído fazendo-se o anodo mais
positivo, ou mais negativo, em relação ao catodo. Seja V
a
diferença de potencial entre o catodo e o anodo. A Fig. 2a
mostra a corrente em
função da ddp (V) para dois valores diferentes da
intensidade da luz incidente
aplicada sobre o catodo. Quando V for positivo, todos os
elétrons emitidos atingem o anodo e a corrente tem o seu valor
máximo.
Observa-se, experimentalmente, que um aumento extra
de V não afeta a corrente. Lenard observou que a corrente
máxima
era proporcional à intensidade da luz. Quando V for negativo, os
elétrons são repelidos pelo anodo. Somente os
elétrons
que tenham as energias cinéticas iniciais mv2/2
maiores
que |eV| podem atingir o anodo. Pela Fig. 2 podemos ver que se V for
menor
que –Vo, nenhum elétron consegue chegar ao anodo. O
potencial
Vo é o potencial frenador o qual está
relacionado
com a energia cinética máxima dos elétrons
emitidos
pela superfície pela relação:
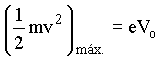
O resultado experimental, da independência de Vo em relação à intensidade da luz incidente, era surpreendente.
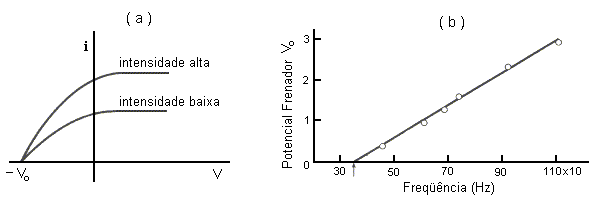
Fig. 2 -
Na visão clássica, o aumento da taxa da energia luminosa incidente sobre a superfície do catodo deveria aumentar a energia absorvida pelos elétrons e deveria, por isso, aumentar a energia cinética máxima dos elétrons emitidos.
Aparentemente, não era o que acontecia. Em 1905, Einstein
demonstrou
que este resultado experimental poderia ser explicado se a energia
luminosa
não fosse distribuída continuamente no espaço, mas
fosse quantizada , como pequenos pulsos, cada qual denominado um
fóton.
A energia de cada fóton é hn ,
onde n é a freqüência e h
a constante de Planck. Um elétron ejetado de uma
superfície
metálica exposta à luz, recebe a energia
necessária
de um único fóton. Quando a intensidade da luz, de uma
certa
freqüência, for aumentada, maior será o número
de fótons que atingirão a superfície por unidade
de
tempo, porém a energia absorvida por um elétron
ficará
imutável. Se f for a energia
necessária
para remover um elétron de uma
superfície metálica, a energia cinética
máxima
dos elétrons emitidos pela superfície será
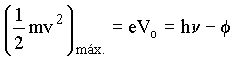
Esta equação é conhecida como a equação do efeito elétrico. A grandeza f é a função trabalho, característica do metal. Alguns elétrons terão energias cinéticas menores que hn -f em virtude da perda de energia que sofrem ao atravessar o metal. A partir da equação do efeito fotoelétrico, podemos ver que o coeficiente angular da reta dá Vo contra n deve ser igual a h/e.
Em resumo podemos ressaltar três pontos importantes da hipótese de Einstein:
![]() - A energia cinética de cada elétron não depende
da
intensidade da luz. Isto significa que dobrando
- A energia cinética de cada elétron não depende
da
intensidade da luz. Isto significa que dobrando
a intensidade da luz teremos mais
elétrons ejetados, mas as velocidades não serão
modificadas.
![]() - Quando a energia cinética de um elétron for igual a
zero
significa que o elétron adquiriu energia
- Quando a energia cinética de um elétron for igual a
zero
significa que o elétron adquiriu energia
suficiente apenas para ser
arrancado
do metal.
![]() - A ausência
de um
lapso de tempo entre a incidência da radiação e a
ejeção
do fotoelétron.
- A ausência
de um
lapso de tempo entre a incidência da radiação e a
ejeção
do fotoelétron.
A verificação experimental da teoria de Einstein era bastante difícil. Experiências cuidadosas de Millikan, publicadas pela primeira vez em 1914, e depois com maior detalhe em 1916, mostraram que a equação de Einstein estava correta e que as medidas de h concordavam com o valor encontrado por Planck.
Os fótons com as freqüências
menores
que o limiar fotoelétrico, e portanto com comprimentos de onda
maiores
que o limiar fotoelétrico em comprimento de onda, não tem
energia suficiente para arrancar um elétron de uma certa
superfície
metálica. O limiar fotoelétrico, e o comprimento de onda
correspondente podem ser relacionados à função
trabalho
f,
igualando-se a zero a energia cinética máxima dos
elétrons
na equação de Einstein.
Problema 1
Uma fonte de luz monocromática a 5500
(Angstrom)
emite 5 watts de radiação. Quantos fótons
são
emitidos a cada segundo ?
|
|
|
|
Problema 2
O limiar de freqüência ou freqüência de corte para a liberação de fotoelétrons no sódio é:
Seguido das descobertas de Planck e Einstein, foram feitos muitos outros experimentos, que só poderiam ser explicados usando o comportamento corpuscular (fótons) da luz. Um desses experimentos é o efeito Compton proposto por A. H. Compton (1923). Compton estudou o espalhamento de raio-X em materiais. Em seus experimentos ele mostrou que a luz espalhada tinha uma freqüência mais baixa do que a incidente, indicando com isto uma perda de energia no processo de espalhamento. Este fenômeno não pôde ser explicado usando a luz como um fenômeno ondulatório. Compton explicou este fenômeno ao estudar a colisão de elétrons com fótons, aplicando as leis de conservação de energia e momento. Veja Fig. 3.

Fig.3 - Espalhamento de Compton
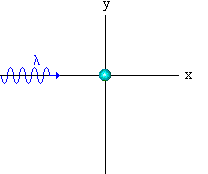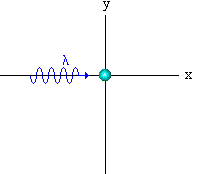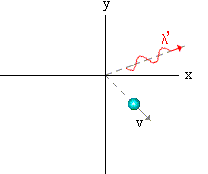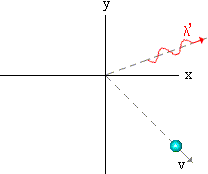
Simulação da colisão elétron+fóton no efeito Compton
Para analisar o efeito Compton, é necessário levar em conta que o efeito é relativístico já que o fóton é uma partícula relativística e viaja à velocidade da luz. Então devemos usar as equações da relatividade para a variação da massa, da energia e do momento linear. A massa m de uma dada partícula é dada por
sendo mo a massa de repouso, c a velocidade da luz.
As energias total antes e depois do choque
são
dadas respectivamente por;
Aplicando a conservação da energia e momento linear,
obtemos:
![]() -
Sobre
a conservação da energia
-
Sobre
a conservação da energia
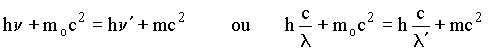
Reorganizando a equação acima e elevando ambos lados ao quadrado obtemos
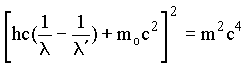
ou
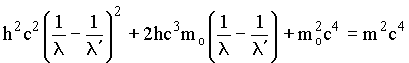 (1)
(1)![]() -
Sobre a conservação do momento linear
-
Sobre a conservação do momento linear
Conservação do momento linear (veja Fig. 1b), componente x e componente y respectivamente
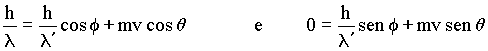
A seguir eliminaremos os termos contendo q nas equações acima. Para isto tomemos o quadrado de ambos lados das duas equações acima.

somando ambas equações,
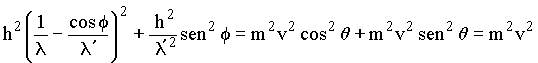
multiplicando por c2 ambos lados da equação acima, temos que
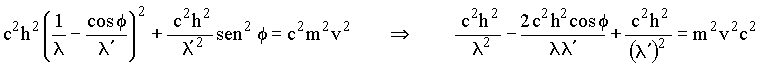 (2)
(2)Subtraindo a equação (2) da equação (1), obtemos
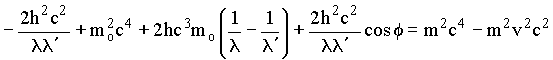 (3)
(3)
O lado direita da equação acima pode ser rescrito por
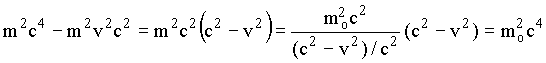
Com isto a equação (3) assume a forma
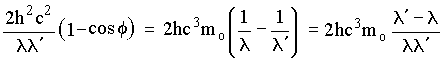
Simplificando ambos lados da equação acima, obtemos
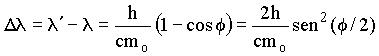
onde temos usado a relação trigonométrica
Definindo 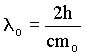 como
sendo o comprimento de onda de Compton, temos que
como
sendo o comprimento de onda de Compton, temos que
Esta é a variação do comprimento de onda e conseqüentemente da freqüência, observado experimentalmente, no choque de um elétron com fóton. Isto significa que realmente o fóton perde energia no choque. Esta energia perdida é transformada em energia cinética usada pelo elétron.
Com isto, mostramos que a
descrição do efeito Compton fica bem estabelecida quando
a sua interpretação é feita a partir do choque
entre
um fóton e um elétron, assumindo o comportamento
corpuscular
da luz.
![]() Voltar
à página principal
Voltar
à página principal ![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta
página
está em constante atualização.
Correções no texto
esugestões
serão bem vindas.
![]() Enviar
mensagens para :
kcmundim@unb.br
Enviar
mensagens para :
kcmundim@unb.br
Last Updated: Jan/10/2002
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Chemistry Institute-UnB, Brasília
BRAZIL
phone: 55 61 307 2150