Aula 20
Molécula de H2 : Teoria do Orbital Molecular
O método orbital-molecular (MO) está
diretamente ligado aos
nomes de Hund na Alemanha, Mulliken
nos Estados Unidos e Lennard-Jones na Inglaterra. Vimos anteriormente que o
método MO trata os
átomos e moléculas dentro da aproximação
dos orbitais. Neste caso, a função de
onda molecular para vários elétrons é aproximada
por um produto de funções mono-eletrônicas
. Numa aproximação simples, pode se dizer que
todos os elétrons são
considerados movendo no campo colombiano de uma
distribuição de núcleos no estado
de equilíbrio. Uma das maiores vantagens do método MO
é que o procedimento
usado na construção da função de onda do
estado fundamental pode ser facilmente
estendido para os níveis superiores ou estados excitados.
No procedimento MO, usa-se em geral o método LCAO “Linear Combination of Atomic Orbitals”. Neste método a função de onda de um elétron é construída de uma combinação linear de orbitais atômicos pertencentes a cada átomo da molécula, isto é;
![]()
onde N
é o número de orbitais atômicos usados na
aproximação. Os quadrados dos coeficientes ![]() , isto
é
, isto
é ![]() ,
representam o peso de uma dado orbital
atômico na construção da função de
onda
molecular e conseqüentemente a probabilidade de se encontrar o
elétron no
orbital molecular
,
representam o peso de uma dado orbital
atômico na construção da função de
onda
molecular e conseqüentemente a probabilidade de se encontrar o
elétron no
orbital molecular ![]() na
vizinhança dos núcleos
pertencentes ao sistema molecular em questão.
na
vizinhança dos núcleos
pertencentes ao sistema molecular em questão.
No
caso particular da molécula de H2, que tem dois
elétrons, a função
de onda para estado fundamental a ![]() é expressa como um
produto de funções mono-eletrônicas,
como a seguir;
é expressa como um
produto de funções mono-eletrônicas,
como a seguir;
![]()
onde ![]() é o orbital molecular
de mais baixa energia. Vimos anteriormente que existem neste caso duas
possíveis combinações lineares dos orbitais
atômicos 1s, que são;
é o orbital molecular
de mais baixa energia. Vimos anteriormente que existem neste caso duas
possíveis combinações lineares dos orbitais
atômicos 1s, que são;
|
|
e |
|
Onde A e B
referem-se
aos dois núcleos de H. Como a molécula é
homo-nuclear tem-se que os coeficientes
C’s são todos iguais. A natureza dos
orbitais ![]() e
e ![]() podem
ser vistas desenhando as superfícies de contorno dessas
duas combinações
lineares. No caso de
podem
ser vistas desenhando as superfícies de contorno dessas
duas combinações
lineares. No caso de ![]() , as
funções de ondas se
somam, isto é interferem-se
construtivamente, na
região entre os núcleos, resultando numa alta
probabilidade de se encontrar um
elétron nesta região. No caso de
, as
funções de ondas se
somam, isto é interferem-se
construtivamente, na
região entre os núcleos, resultando numa alta
probabilidade de se encontrar um
elétron nesta região. No caso de ![]() , as
funções de ondas se cancelam (interferem-se
destrutivamente) na região entre os núcleos, resultando
em um nó nesta região.
Veja superfície de contorno na Fig. 1(b).
, as
funções de ondas se cancelam (interferem-se
destrutivamente) na região entre os núcleos, resultando
em um nó nesta região.
Veja superfície de contorno na Fig. 1(b).
Um
elétron no
orbital ![]() , com alta
densidade eletrônica entre os
núcleos, tem energia mais baixa que um elétron no
átomo de hidrogênio isolado;
então,
, com alta
densidade eletrônica entre os
núcleos, tem energia mais baixa que um elétron no
átomo de hidrogênio isolado;
então, ![]() é
denominado de orbital ligante.
Um elétron no orbital
é
denominado de orbital ligante.
Um elétron no orbital ![]() , com um nó entre os
núcleos e região de alta densidade eletrônica
afastada dos núcleos, tem energia
maior que um elétron no átomo isolado; então ele
é denominado de orbital anti-ligante.
, com um nó entre os
núcleos e região de alta densidade eletrônica
afastada dos núcleos, tem energia
maior que um elétron no átomo isolado; então ele
é denominado de orbital anti-ligante.
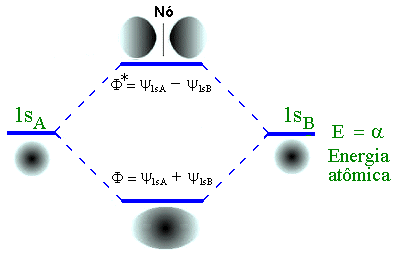
Fig.2- Diagrama de energia para a molécula de H2.
![]()
Esta função é simétrica, isto é ![]() . Mas de acordo com o
princípio da exclusão de Pauli
a função de onda final
deve ser anti-simétrica. Neste caso a questão de
anti-simetria é resolvida
introduzindo as funções de spin.
. Mas de acordo com o
princípio da exclusão de Pauli
a função de onda final
deve ser anti-simétrica. Neste caso a questão de
anti-simetria é resolvida
introduzindo as funções de spin.
Molécula de H2 : Estado Excitado
Vimos anteriormente que uma das maiores vantagens do método MO está no fato de que os procedimentos usados no cálculo do estado fundamental podem ser estendidos para os estados excitados. Neste caso os orbitais atômicos usados na construção dos estados excitados são 1s, 2s, 2px, 2py e 2pz. Uma das aproximações mais simples é considerar apenas as somas e diferenças entres os orbitais idênticos o que leva ao seguinte diagrama de energia,
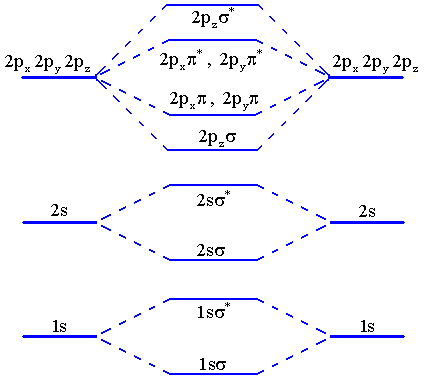
Fig.3 – Diagrama de energia para alguns estados excitados de H2
Método de Hückel
A método de Hückel pode ser considerada o pai das aproximações na teoria do orbital molecular. Ele foi formulado por volta de 1930 por Hückel. Esta teoria se limita aos sistemas p conjugados. Como a teoria de Hückel foi formulada inicialmente, não se encontra muitas aplicações nas pesquisas de hoje, mas ela pode ser usada no sentido prover informações qualitativas sobre propriedades eletrônicas de uma classe grande sistemas moleculares. Além disso, a teoria de Hückel é vastamente usada para propósitos educativos já que ela pode ser resolvida, na maioria dos casos, sem ajuda de computadores.
Um artigo interessante que discute as interações eletrônicas foi escrito por Kenichi Fukui como uma aula magna apresentada à comunidade científica no recebimento de seu prêmio Nobel. Este arquivo pode ser obtido no anexo a seguir. ANEXO.
Em nossas discussões trataremos o caso de sistemas moleculares
conjugados do
tipo p,
nos quais existe alternância de ligações
químicas simples e duplas ao longo da
cadeia de átomos de carbono. Neste caso, os diagramas de energia
para os
orbitais moleculares do tipo p podem ser tratados dentro desta teoria de uma
forma
muito simples quando se comparado com os métodos convencionais.
Todos os átomos
de carbono são tratados de forma idêntica, o que significa
que as integrais
responsáveis pelas interações de Coulomb
são iguais. Por exemplo, no eteno e no
butadieno, assumimos as
ligações do tipo s como
fixas, e nos concentramos no cálculo da energia das
ligações do tipo p.
De acordo com o modelo de Hückel os orbitais p são expressos como combinação linear dos orbitais atômicos (LCAO-Linear Combination of Atomic Orbitals) do carbono 2p, que estão perpendiculares ao plano molecular, que na sua forma geral é expressa por;
![]()
Sendo N o número de orbitais atômicos considerados na aproximação. Sabemos também que o operador hamiltoniano leva-se em conta apenas os termos mono-eletrônicos, isto é
![]()
A soma é sobre todos os elétrons. Desde que todos os orbitais, neste caso, é duplamente ocupado a energia molecular total será igual a duas vezes a soma das energias relativas a cada orbital, isto é;
![]()
Onde m é numero de orbitais moleculares duplamente ocupados, cujo digrama de energia é igual a;
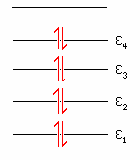
No caso do eteno,
tem-se dois átomos de carbono, assim o orbital molecular tem a forma,
![]()
O nosso objetivo é buscar os orbitais moleculares que minimize a energia molecular, usando a mesma metodologia da aula-18. Matematicamente isto significa que,
![]()
Usando
a mesma metodologia para o caso da molécula de ![]() , tem-se que,
, tem-se que,
![]()
![]()
onde,
|
|
e |
|
Neste
caso assumimos que,
|
|
|
|
e |
|
Substituindo estes valores no sistema de equações acima, temos que;
![]()
![]()
Este é um sistema de equações homogêneo que pode ser resolvido pelo determinante secular,
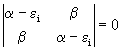
O que leva as relações;
![]()
Para i =1 tem-se que,
![]()
![]()
o que implica
em ![]() .
Usando o fato de que a função de onda molecular tem que
ser normalizada,
encontra-se que
.
Usando o fato de que a função de onda molecular tem que
ser normalizada,
encontra-se que ![]() . Em resumo, as
energias e orbitais moleculares podem ser escritos por,
. Em resumo, as
energias e orbitais moleculares podem ser escritos por,
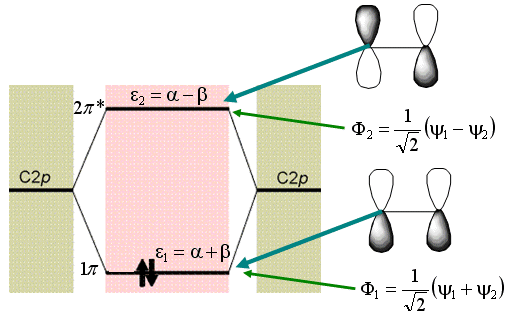
A diferença de energia entre os estados fundamental e excitado é igual a;
![]() .
.
O parâmetro ![]() é
usualmente escolhido de forma que
é
usualmente escolhido de forma que ![]() seja igual ao pico da
banda
absorção experimental.
seja igual ao pico da
banda
absorção experimental.
Método de Hückel : Molécula de Butadieno
Como exercício, e com base no método variacional discutido na aula-18, mostre que, para o butadieno, o modelo de Hückel fornece quatro funções como a seguir,
![]() onde i =1, 2, 3 e 4
onde i =1, 2, 3 e 4
Para isto é necessário encontrar os coeficientes (C´s) da função de onda que minimize o funcional energia. O que leva ao seguinte determinante secular,
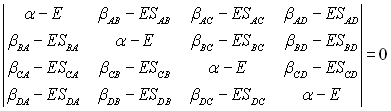
que após as seguintes aproximações;
i. Todas integrais de recobrimento (overlap) são assumidas iguais a zero.
ii. Todas as integrais de ressonância entre átomos não vizinhos são iguais a zero.
iii. As integrais de ressonância restantes são iguais a
![]() .
.
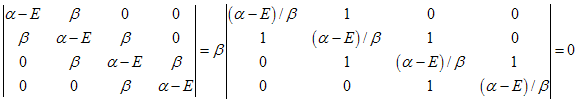
Por outro lado pode ser escrito como uma combinação de determinantes de terceira ordem como a seguir:
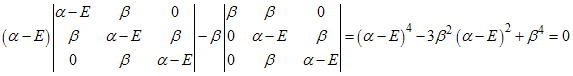
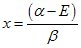 , assim
temos que
, assim
temos que
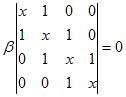
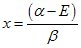 , assim o
determinante é
igual a um polinômio de quarto grau, isto é,
, assim o
determinante é
igual a um polinômio de quarto grau, isto é,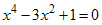
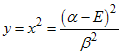 , temos que
, temos que
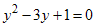
Resolvendo
este polinômio e usando a relação 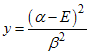 encontramos
quatro valores para a energia, isto é,
encontramos
quatro valores para a energia, isto é,
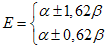
A energia de delocalização, a qual indica a estabilização relativa da molécula é dada pela relação;
![]()
O
diagrama de energia para o butadieno
é igual
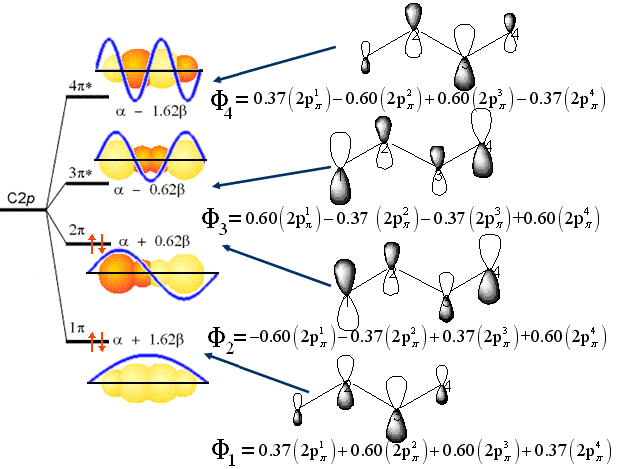
Os
orbitais moleculares F1, F2, F3 e F4
são esboçados tri-dimensionalmente
como a seguir,
|
Orbital F1 |
Orbital F2 |
|
Orbital F3 |
Orbital F4 |
Propriedades
eletrônicos
Com
determinação da função onda e dos
coeficientes LCAO´s ( 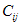 )
podemos definir várias
propriedades eletrônicas dos sistemas moleculares descrito pelo
modelo de Hückel, como a seguir.
)
podemos definir várias
propriedades eletrônicas dos sistemas moleculares descrito pelo
modelo de Hückel, como a seguir.
A carga atômica
de um dado átomo A
qualquer é definido pela relação
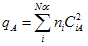
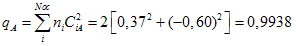
Podemos
introduzir também o conceito de índice de
ligação 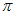 entre os átomos A e B o qual é definido pela
relação,
entre os átomos A e B o qual é definido pela
relação,
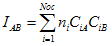
No caso do butadieno o índice de ligação entre os átomos A e B é dado pela relação,