Aula 19
![]() - Interpretação Física da Função de
Onda Molecular
- Interpretação Física da Função de
Onda Molecular
Na seção anterior discutimos as características dos dois orbitais moleculares do íon H2+ que têm a menor energia. Pela resolução da equação de Schrödinger, para o movimento de um elétron sujeito ao campo de dois prótons fixos, é possível obter descrições exatas, se bem que bastantes complicadas, dos orbitais moleculares do H2+. Vimos também que uma descrição matematicamente muito mais simples, apesar de ser definitivamente uma aproximação, pode ser obtida encarando estes orbitais moleculares como Combinações Lineares de Orbitais Atômicos (LCAO-MO). Isto significa simplesmente que para encontrar a função de onda do orbital molecular efetuamos a combinação linear (soma ou subtração) da função de onda do orbital atômico de um átomo com a função de onda de orbital atômico do outro átomo. Temos então, para dois núcleos a e b,
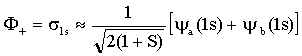
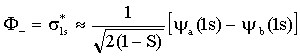
Os fatores que multiplicam a soma de funções de onda
são fatores que normalizam a função de onda molecular de maneira que a
probabilidade de se encontrar um elétron em algum lugar do espaço é igual a
unidade. A quantidade S denomina-se integral de co-partilhamento e é, de
maneira explícita igual a;
![]()
A integral de co-partilhamento S é uma medida de quão
intimamente as duas funções de onda atômicas coincidem, ou estão superpostas.
Usualmente S é positivo e aproximadamente igual a 0,2 ou 0,3. Em relação as
funções de ondas acima, pode-se observar o seguinte,
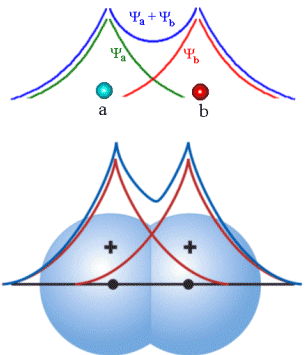
Fig. 3 Função de onda atômica e molecular, estado ligante
A figura (4) abaixo mostra
a densidade eletrônica de cada átomo isolado assim como da molécula.
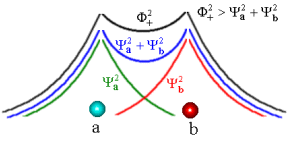
Fig. 4 Densidade eletrônica no átomo e na molécula
O orbital molecular
descrito pela função F- é denominado anti-ligante, pois
![]()
As figuras abaixo
referem-se a este caso,.
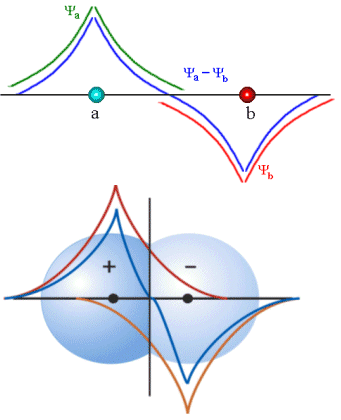
Fig. 5 Função de onda atômica, estado antiligante
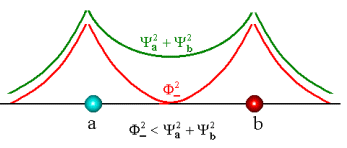
Fig.6 Densidade eletrônica atômica e molecular
![]() - Energia dos Orbitais
Moleculares
- Energia dos Orbitais
Moleculares
Conhecendo a função de onda molecular pode-se calcular a energia molecular,
através da operação,
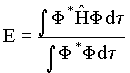
Pela condição de
normalização tem-se que 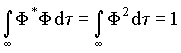 , logo a energia assume a forma,
, logo a energia assume a forma,
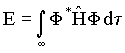
Como existem duas funções de onda, F+ e F_ , deve-se necessariamente ter dois
valores distintos para a energia molecular, isto é
![]()
Mais explicitamente estas
duas energias podem ser obtidas resolvendo-se as seguintes integrais,
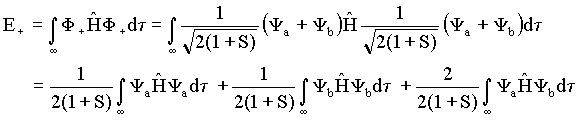
onde
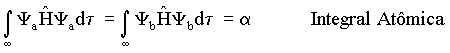 ,
,
esta integral é equivalente
a energia do elétron em um átomo de hidrogênio isolado. Como o elétron está
ligado ao átomo o a é negativo ( a < 0).
Tem-se ainda que
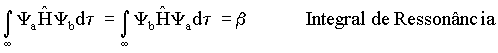
onde b representa a diminuição de energia devido a formação do orbital
molecular, em outras palavras b descreve a redistribuição
eletrônica em torno dos núcleos atômicos pertencentes à molécula. b também é negativo (b < 0).
Substituindo a e b na equação para energia temos que
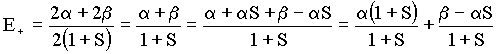
e daí
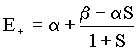
Como tem-se que E+ < a . Isto mostra que o elétron é mais
estável em uma orbital molecular ligante (1ss) do que em um orbital atômico 1s.
tem-se que E+ < a . Isto mostra que o elétron é mais
estável em uma orbital molecular ligante (1ss) do que em um orbital atômico 1s.
Procedendo-se de forma equivalente ao caso anterior, pode-se mostrar que a
energia do estado anti-ligante é igual a
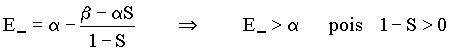
Neste caso, percebe-se que o elétron em um orbital molecular anti-ligante (1ss *) tem energia maior que o mesmo
elétron em um orbital atômico 1s. A figura abaixo mostra o diagrama de
energia molecular em relação as energias dos átomos em separado.
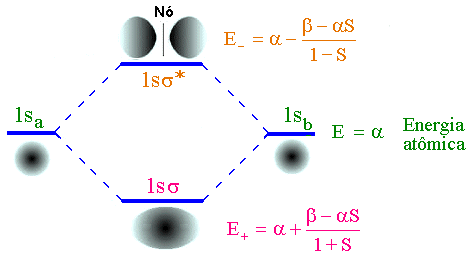
Fig. 7 - Diagrama de energia para a molécula de H2+
O mínimo de energia E+
justifica a existência da ligação química no íon molecular H2+.
A energia E- é sempre maior que a energia do orbital atômico a (E- > a ) e corresponde a um estado
excitado. A função F- não corresponde a um estado estável para o íon
H2+.
![]() - Orbitais e as Ligações Químicas
- Orbitais e as Ligações Químicas
Vimos nas seções anteriores que os orbitais moleculares podem ser construídos
como uma combinação linear dos orbitais atômicos e eles são populados por um
único elétron ou um par de elétrons. Quando dois orbitais atômicos
equivalentes, Ya e Yb, se combinam, eles sempre produzem um orbital
ligante e um anti-ligante. Veja fig. 8.
O orbital ligante ![]() é caracterizado por uma superposição (em inglês
overlap) positiva e por densidade eletrônica localizada na região entre os
núcleos. Contrariamente, o orbital anti-ligante
é caracterizado por uma superposição (em inglês
overlap) positiva e por densidade eletrônica localizada na região entre os
núcleos. Contrariamente, o orbital anti-ligante ![]() não exibe um "overlap"
e uma superfície nodal na região entre os núcleos. Quando Ya e Yb são
orbitais do tipo s a combinação ligante é dada por Ya + Yb e a
anti-ligante por Ya - Yb .
não exibe um "overlap"
e uma superfície nodal na região entre os núcleos. Quando Ya e Yb são
orbitais do tipo s a combinação ligante é dada por Ya + Yb e a
anti-ligante por Ya - Yb .
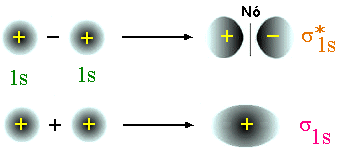
Fig. 8 - Orbitais moleculares formados a partir de orbitais atômicos do tipo s.
|
Tipos de Orbitais |
Características |
|
|
· Energia alta · Instável · Eletronicamente desfavorável ·
Elétrons situados externamente aos núcleos |
|
|
|
|
|
· Energia baixa · Estável · Eletronicamente favorável ·
Elétrons situados entre os núcleos |
Quando Ya e Yb são orbitais do tipo p interagindo de
uma forma s e orientados como mostra a figura abaixo, a
ligação é do tipo ligante e novamente o orbital molecular será uma combinação
do tipo Ya + Yb e o anti-ligante Ya - Yb .
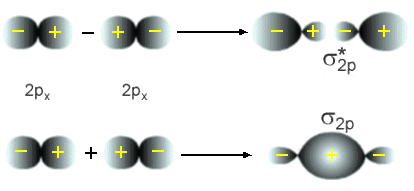
Fig. 9 - Ligações formadas pela superposição de 2 orbitais atômicos do tipo p
formando orbitais s.
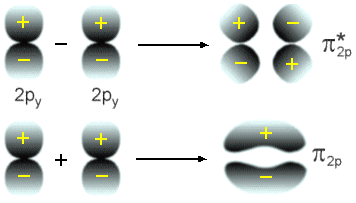
Fig. 10 - Ligações formadas pela superposição de 2 orbitais
atômicos do tipo p formando orbitais p.
![]() - Distribuição Eletrônica nas
Ligações Químicas
- Distribuição Eletrônica nas
Ligações Químicas
Em termos da distribuição
de cargas eletrônicas na ligações químicas temos basicamente os seguintes
tipos:
|
Na+ Cl-
|
|
Ligação Iônica |
|
Cl : Cl
|
|
Ligação covalente não-polar |
|
d+H - Cl d- [H : Cl]
|
|
Ligação covalente polar |
Listaremos abaixo a representação 3-dimensional de alguns
orbitais atômicos não convencionais.
|
Orbital do tipo s, p e d |
Orbital do tipo f |
|
Orbital do tipo g |
Orbital do tipo h |