Aula 18
![]() - Aproximação de Born-Oppenheimer
- Aproximação de Born-Oppenheimer
Discutimos anteriormente as dificuldades de se resolver a equação de Schrödinger no caso de sistema moleculares. Em particular vimos que apenas o átomo de hidrogênio pode ser resolvido exatamente. Sistemas moleculares poliatômicos não têm soluções exatas para a equação de Schrödinger. Para isto é necessário fazer-se certas aproximações ou simplificações nesta teoria a fim de tornar o problema molecular solúvel dentro da formulação de Schrödinger. Uma destas aproximações mais adotada é a aproximação de Born-Oppenheimer a qual estabelece que os núcleos estão fixos na molécula. Esta aproximação é viável devido ao fato de que os núcleos são mais pesados que os elétrons.
![]() - Moléculas Diatômicas Homonucleares
- Moléculas Diatômicas Homonucleares
De uma maneira geral toda ligação formada por emparelhamento de elétrons é uma ligação covalente. Tomemos, por exemplo, a molécula de hidrogênio; os elétrons dos dois átomos de hidrogênio são compartilhados pelos dois núcleos H. Os dois elétrons não distinguem um núcleo do outro.
A molécula é formada por dois núcleos ligados entre eles pelo intermediário de dois elétrons.
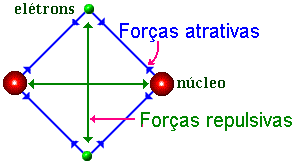
Fig. 1
A distância inter-nuclear
(d = 0,74 Å) corresponde ao equilíbrio do sistema prótons
+ elétrons. As forças orbitais neste próton-elétron,
equilibram as forças repulsivas próton-próton e elétron-elétron,
para isto os elétrons têm a tendência de se concentrarem
na região entre os núcleos. As forças em jogo são
forças eletrônicas, mas não é possível explicar
a existência e a estabilidade da molécula somente com a ajuda
da eletrostática clássica. Em particular, ela não
consegue explicar a distribuição eletrônica em torno
dos núcleos. Para resolver este problema devemos recorrer a Mecânica
Quântica que leva em conta o caráter ondulatório dos elétrons
no átomo.
![]() - Orbitais Moleculares Mono-eletrônicos
- Orbitais Moleculares Mono-eletrônicos
Em um átomo, cada elétron é descrito por um orbital atômico Y . Em uma molécula, cada elétron será descrito por uma função de onda F denominado orbital molecular. A teoria dos orbitais moleculares repousa sobre princípios análogos à aqueles que vimos para os átomos, isto é,
a)- A função de onda F ou orbital molecular tem o mesmo significado que o orbital atômico. O quadrado do módulo de F , isto é |F|2, representa a densidade de probabilidade de presença eletrônica. A função de onda deve ser, portanto, normalizada,
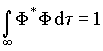
b)- A cada função de onda F corresponde uma energia bem definida. A soma das energias de cada elétron, levando em conta as conexões relativas à interação entre os elétrons, representa a energia total da molécula.
c)- Os elétrons ocupam diferentes níveis de energia por ordem crescente de energia. O princípio da exclusão de Pauli é aplicado em todo sistema eletrônico, atômico e molecular. Cada elétron tem um spin. Desta maneira, para cada orbital molecular F deve-se ter no máximo dois elétrons tendo spins opostos.
Na teoria do Orbital Molecular (MO) os elétrons são tratados como se estivessem espalhados pela molécula como um todo e não ligados especificamente a cada um dos núcleos que compõem a molécula. Existem obviamente, outras teorias que tratam das interações eletrônicas nas moléculas e uma delas é a Teoria da Ligação de Valência (VB-valence Bond Theory). Apesar de que a teoria VB tenha surgido primeiro que a MO está última tem sido mais usada nos cálculos de propriedades moleculares. Para introduzi-la, estudaremos a seguir o sistema molecular mais simples que é o íon molecular H2+.
![]() - O estudo do íon H2+ :
- O estudo do íon H2+ :
Tratamento do ion H2+
pelo método LCAO (Linear Combination of Atomic Orbitals)
Em uma molécula, quando o elétron se situa nas vizinhanças de um núcleo ele é submetido somente à atração do núcleo. Desta maneira o orbital atômico que descreveria o movimento eletrônico em um átomo isolado, constitui uma função aproximada para descrever o elétron na molécula na vizinhança imediata dos núcleos. Em conseqüência, os orbitais atômicos Y1s do hidrogênio poderão servir de base para a construção dos orbitais moleculares.
Nós vamos supor então que a função de onda F , que descreve o elétron na molécula de H2+, é descrita por uma combinação linear de orbitais atômicos Ya e Yb de átomos de hidrogênio isolados a e b;
![]()
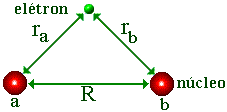
Fig. 2
A equação de Schrödinger para o sistema molecular em Unidades Atômicas (u.a.) tem a forma,
![]() (1)
(1)
onde![]() é
o operador Hamiltoniano e é dado pela relação,
é
o operador Hamiltoniano e é dado pela relação,
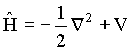 (2)
(2)
sendo V o potencial eletrostático devido as interações elétron-próton, os dois primeiros termos da equação (3) e próton-próton o terceiro temo,
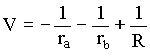 (3)
(3)
Assim a equação de Schrödinger assume a forma
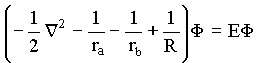 |
|
|
Está é a equação
de Schrödinger para a molécula de H2+
que temos que resolver. Como podemos observar ela é uma equação
diferencial de segunda ordem no espaço. Notamos também que
o tempo não aparece nesta equação. Isto deve-se ao
fato de estarmos estudando o referido sistema molecular num instante t
qualquer.
Vimos, em aulas anteriores,
que devido ao fato da Mecânica Quântica ser um teoria probabilística
as grandezas físicas observadas devem ser calculadas na média.
Assim, a energia média deste sistema molecular deve satisfazer a
relação,
![]() (5)
(5)
ou
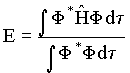 (6)
(6)
Se as funções de ondas moleculares são orto-normalizadas a integral no dividendo da equação (6) deve ser igual a um.
![]() - Combinação Linear de Orbitais
Atômicos (LCAO)
- Combinação Linear de Orbitais
Atômicos (LCAO)
Se o elétron pode ser encontrado, com igual probabilidade, em um orbital atômico no átomo A assim como num orbital no átomo B, a função de onda que contemple estes dois casos deve ser construída com uma combinação linear dos dois orbitais atômicos, como se segue:
![]() (7)
(7)
Onde Ya e Yb são, respectivamente, as funções de ondas para os orbitais 1s dos dois átomos (A e B) em separados. Existem várias formas de resolver este problema dentro da teoria MO, isto é de determinar os coeficientes Ci que melhor descreva as propriedades moleculares. A seguir vamos aplicar um desses métodos para determinar os Ci, o qual é denominado método variacional. Este método consiste em escolher uma função F de modo que um valor mínimo para a energia molecular seja obtido. No caso do íon de H2+ , que é uma molécula homo-nuclear, tem-se,
![]() (8)
(8)
cuja energia é igual a
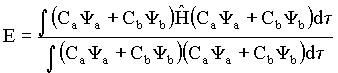 (9)
(9)
ou de uma forma mais simplificada, temos que E assume a forma
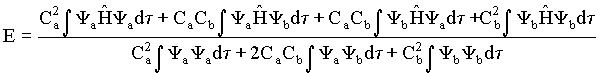 (10)
(10)
Como não existe distinção entre os núcleos a e b, pois H2+ é homo-nuclear, tem-se,
![]() (11)
(11)
Designando
|
|
|
e assumindo que as funções Ya e Yb são soluções da equação de Schrödinger para os átomos a e b separados, temos que
|
|
|
|
Daí tiramos que a energia total é igual a
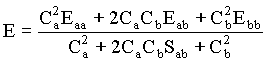 (14)
(14)
Vemos na equação acima que a energia molecular total é função dos coeficientes Ca e Cb usados na expansão do orbital molecular em termos dos orbitais atômicos. Com isto, estamos assumindo, mais tarde demonstraremos que isto é verdade, que as funções de onda para os orbitais atômicos Y formam uma base de um espaço vetorial, o que justifica utilizá-los na descrição dos orbitais moleculares F . Isto quer dizer F pode ser escrito como uma combinação linear dos Y .
Então, para se obter a energia molecular mínima, basta derivar E em função dos coeficientes Ca e Cb, como a seguir;
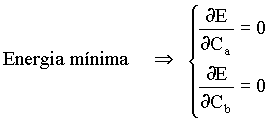 (15)
(15)
Usando a regra de derivação da razão entre duas funções, tem-se que;
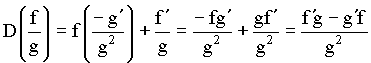 (16)
(16)
Aplicando esta regra para calcular as derivas da energia em função dos coeficientes Ca e Cb, obtemos
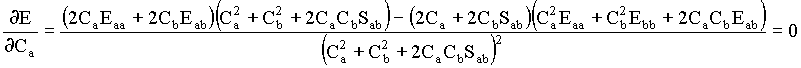
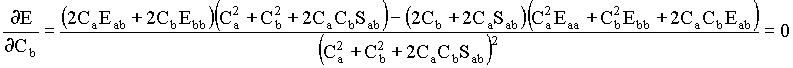
As duas equações acima podem ser reorganizadas da seguinte forma,
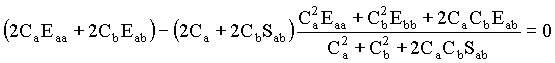
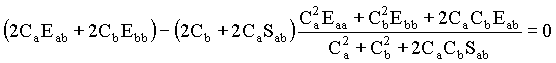
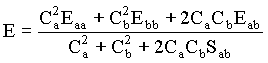
Substituindo esta expressão para a energia nas equações referentes as derivadas de E em função dos coeficientes temos que,
![]()
![]()
Que podem ser reescritas como:
|
|
Este resultado pode ser expresso na seguinte forma matricial
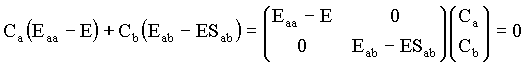
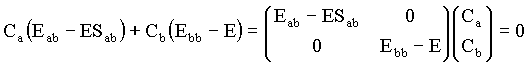
Onde Ca e Cb são os coeficientes a serem determinados para que a condição de energia mínima. O conjunto das duas equações acima formam um sistema de duas equações e duas incógnitas, equivalente ao sistema de equações;
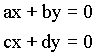
cuja solução trivial é dada por x = y = 0. A solução não trivial pode ser obtida da seguinte forma,
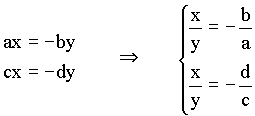
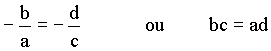
Esta solução é equivalente ao cálculo do seguinte determinante
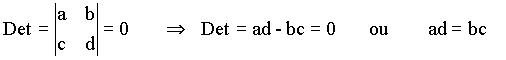
e para o caso das energias tem-se;
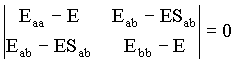
Calculando o determinante desta matriz obtemos a seguinte relação envolvendo a energia total,
![]()
Para o ion molecular de hidrogênio os núcleos atômicos são idênticos, com isto tiramos que
Eaa = Ebb, então a equação acima pode ser reescrita como,
![]()
Esta é uma equação de segundo grau em E. Neste caso particular ela é equivalente a,
![]()
Daí podemos mostrar que existem dois valores possíveis para E (energia molecular total), isto é,
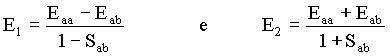
Vimos anteriormente que
![]()
Então, no caso em que E = E1, podemos encontrar uma relação entre os coeficientes, como a seguir
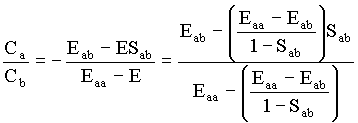

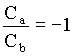
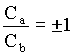
Com isto mostramos que existem duas funções possíveis funções de onda que são soluções da equação de Schrödinger para este problema, isto é
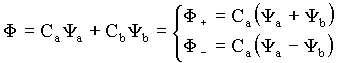
![]() - Condições de Normalização
- Condições de Normalização
A condição de normalização estabelece que a probabilidade de encontrar o elétron em qualquer ponto do espaço, isto é em um volume infinito, deve ser igual a 1. Matematicamente isto significa que a integral do quadrado da função de onda, deve ser igual a 1 quando integrada em um volume infinito. Então,
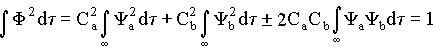
De forma similar esta condição de normalização deve ser válida no caso em que o elétron se encontra em um dos orbitais atômicos, isto é
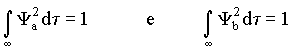
A integral 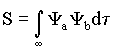 mede a importância do recobrimento entre os orbitais Ya
e Yb. Esta integral descreve a superposição
eletrônica devido a interação entre os dois átomos
da molécula de H2+. Usando ainda o fato de
que os coeficientes Ca e Cb são iguais temos
que
mede a importância do recobrimento entre os orbitais Ya
e Yb. Esta integral descreve a superposição
eletrônica devido a interação entre os dois átomos
da molécula de H2+. Usando ainda o fato de
que os coeficientes Ca e Cb são iguais temos
que
![]()
Desta equação pode-se determinar os coeficientes C usados na expansão da função de onda molecular, isto é
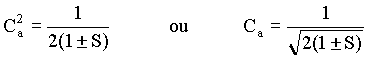
Substituindo este resultado na equação para a função de onda molecular, temos que
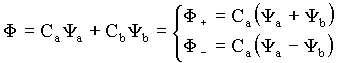
ou
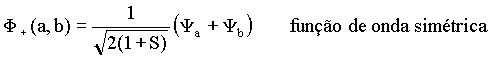
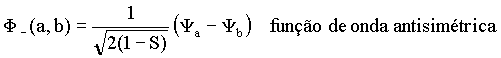
A função de onda simétrica (F+) fica inalterada ao trocar Ya por Yb. No caso da função anti-simétrica (F-) a troca de Ya por Yb implica em uma mudança de sinal em F-. Isto significa que
![]()
![]() Voltar
à página principal
Voltar
à página principal ![]() Voltar
ao início desta página
Voltar
ao início desta página
![]()
O conteúdo desta página
está em constante atualização.
Correções no texto e sugestões
serão bem vindas.
![]() Electronic
Address :
kleber@unb.br
Electronic
Address :
kleber@unb.br
Last Updated: Sep/13/2000
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No 169.766 -
Biblioteca Nacional - Ministério da Cultura
phone: 55 61 307 2150
FAX 55 61 307 21 50