Aula-17
Átomos Hidrogenóides
 (1)
(1)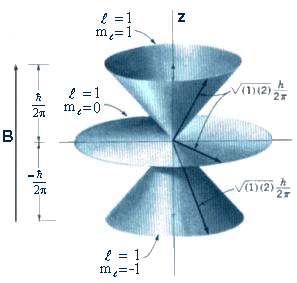
Fig.1
Observe que o número quântico n
controla os valores máximos de ![]() que estabelece limites de variações para o
que estabelece limites de variações para o ![]() .
Para descrever completamente um estado eletrônico é necessário
introduzir mais dois números quânticos relativos ao spin eletrônico.
Estes números são s e ms, sendo
.
Para descrever completamente um estado eletrônico é necessário
introduzir mais dois números quânticos relativos ao spin eletrônico.
Estes números são s e ms, sendo ![]() e
e ![]() .
.
![]() 2- Camadas e subcamadas
2- Camadas e subcamadas
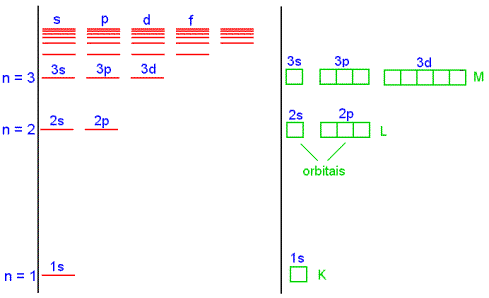
Todos orbitais relativos a um valor de n são ditos formar uma única camada no átomo. No átomo de hidrogênio todos orbitais, para um mesmo valor de n, têm o mesmo valor de energia, de acordo com a equação (1).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
2 |
4 |
|
|
|
|
|
|
p |
1 |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||
|
M |
3 |
9 |
|
|
|
|
|
|
p |
1 |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||
|
d |
2 |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
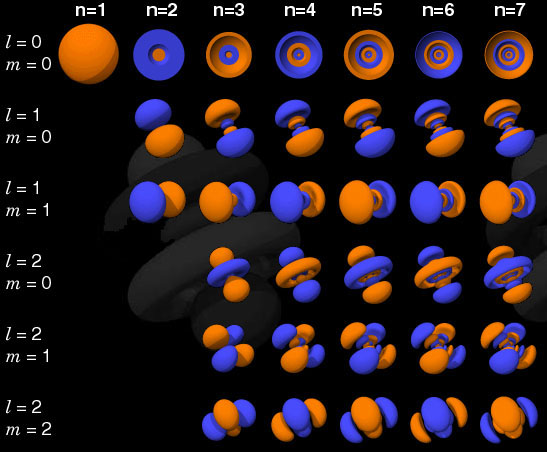
Densidade de probabilidade em função dos números quânticos n, ![]()
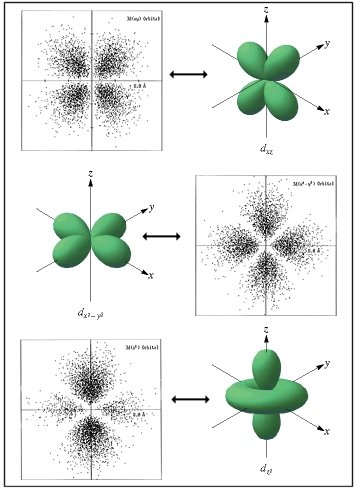
Densidades de probabilidades relativas aos orbitais tipo d
![]() 3- Orbitais do tipo s
3- Orbitais do tipo s
O orbital
com ![]() é dito representar o estado fundamental ou de mais baixa energia
o qual é descrito pela função de onda;
é dito representar o estado fundamental ou de mais baixa energia
o qual é descrito pela função de onda;
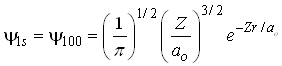
Como este orbital depende apenas da coordenada r então, ele é um orbital esfericamente simétrico. Já o orbital 2s é descrito pela equação;
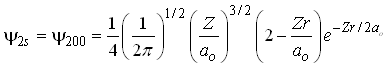
Generalizando, podemos dizer que todos os orbitais do tipo s são dependentes apenas da coordenada r e são portanto esfericamente simétricos.
Em particular o orbital 2s tem um nó,
isto é a função de onda tem um ponto em que ela é
igual a zero, isto é ![]() Isto implica que,
Isto implica que,
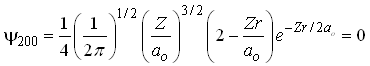
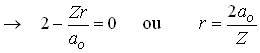
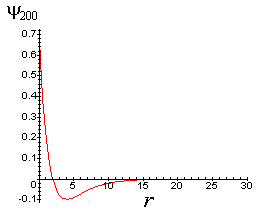
Fig. 2- Orbital 2s contém um nó
Assim ![]() é o ponto onde a função de onda se anula, isto
é, o ponto onde ela tem um nó.
é o ponto onde a função de onda se anula, isto
é, o ponto onde ela tem um nó.
Similarmente, pode-se mostrar que o orbital 3s igual a
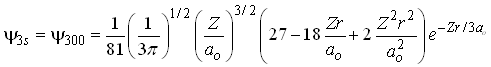
tem dois nós, nos seguintes pontos;
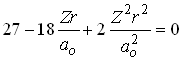
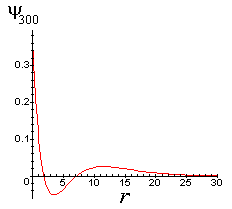
Fig. 3 - Orbital 3s contém dois nós
![]() 4- Cálculo do raio médio de
um orbital 1s
4- Cálculo do raio médio de
um orbital 1s
Por definição de valor médio de uma grandeza observável, temos que;
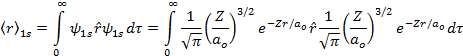
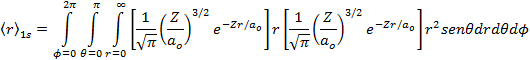
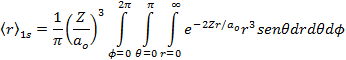
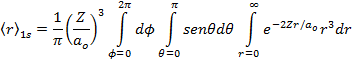
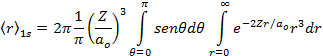
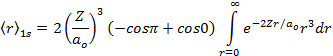
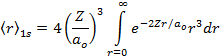
![]()
![]()
![]() 5- Função distribuição radial para um orbital 1s
5- Função distribuição radial para um orbital 1s
Podemos
perguntar também qual é a probabilidade de encontrar o elétron
numa certa região em torno do núcleo. Esta questão
pode ser respondida calculando o módulo da função
de onda ao quadrado ![]() .
Daí tiramos que;
.
Daí tiramos que;
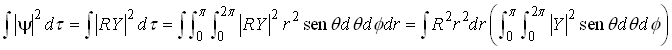
Lembre-se que;
Daí tiramos que;
![]()
Assim, a probabilidade P(r) é igual a
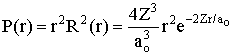 .
.
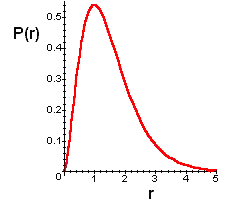
Fig. 4 - Distribuição radial
![]() 6- Calculando o raio mais provável para
orbital 1s
6- Calculando o raio mais provável para
orbital 1s
Para calcular o raio mais provável, basta derivar a função P(r) e igualar o resultado à zero, isto é
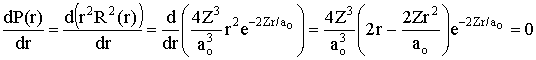
e então,
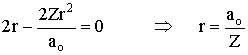
Deste resultado, podemos montar uma tabela para o
cálculo do raio mais provável para os seguintes íons;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|