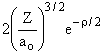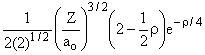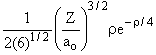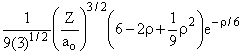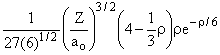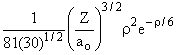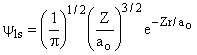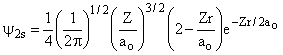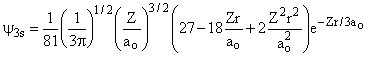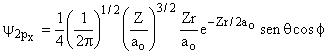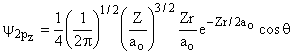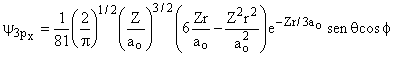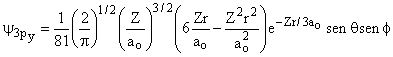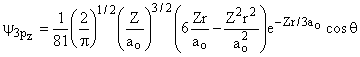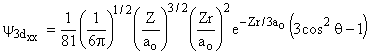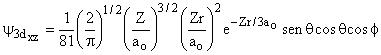Aula-16
- Átomo de Hidrogênio usando a Massa Reduzida.
Até o momento temos considerado, no átomo, apenas o movimento eletrônico. Nesta seção vamos levar em conta a influência do movimento nuclear no átomo de hidrogênio o qual contém um núcleo (positivo) e um elétron (negativo). O núcleo tem massa mn e o elétron massa me.
Para facilitar a compreensão deste problema vamos estudar, inicialmente, o caso clássico de duas partículas interagentes com massas mn e me respectivamente, veja Fig.1.
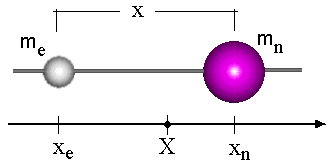
De acordo com a mecânica clássica a energia total deste sistema é uma soma das energias cinéticas da partícula 1 (elétron) e da partícula 2 (núcleo), e o potencial (V) de interação entre elas, a qual pode ser expressa da seguinte forma;
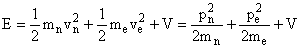 (1)
(1)
O centro de massa deste sistema está localizado em uma posição X, dada pela equação;
![]() (2)
(2)
Temos também a seguinte equação de vínculo envolvendo as distâncias entre as partículas;
![]() (3)
(3)
onde x = xe - xn. Conseqüentemente o momento linear pode ser re-escrito em função destas novas variáveis, como a seguir:
![]() (4)
(4)
Destas duas últimas equações podemos tirar que;
![]() (5)
(5)
onde ![]() é a massa
reduzida do sistema de duas partículas. Usando as regras de quantização podemos
construir o operador Hamiltoniano para um sistema equivalente, isto é;
é a massa
reduzida do sistema de duas partículas. Usando as regras de quantização podemos
construir o operador Hamiltoniano para um sistema equivalente, isto é;
![]() (6)
(6)
e a equação de Schrödinger fica igual a;
![]() (7)
(7)
Podemos separar o movimento total em duas partes, uma relativa ao centro de massa e outra referente às coordenadas relativas, como a seguir;
![]() (8)
(8)
![]() (9)
(9)
com ![]() . Isto implica que a
função de onda também pode ser escrita como um produto de funções relativas aos
movimentos do centro de massa e das coordenadas relativas, isto é;
. Isto implica que a
função de onda também pode ser escrita como um produto de funções relativas aos
movimentos do centro de massa e das coordenadas relativas, isto é;
![]() (10)
(10)
No caso do átomo de hidrogênio o potencial V de interação entre as duas partículas é o potencial coulombiano, dado por;
![]() (11)
(11)
Conseqüentemente a equação de Schrödinger referente as coordenadas relativas, é igual a;
![]() (12)
(12)
Como o sistema tem simetria esférica, a equação diferencial acima fica mais simples de ser resolvida se for escrita num sistema de coordenadas que seja apropriada à simetria do problema, que neste caso é esférica. Assim, devemos escrever o operador Laplaciano e conseqüentemente a equação de Schrödinger neste sistema de coordenadas, isto é,
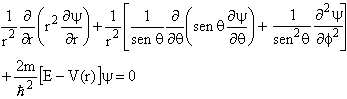 (13)
(13)
Os estados energéticos deste sistema são determinados pelas
soluções desta equação diferencial, cujas soluções são continuas, têm derivadas
contínuas em r, ![]() e
e ![]() e são ainda, para os estados ligados, de quadrado integrável.
e são ainda, para os estados ligados, de quadrado integrável.
As soluções da equação (13) podem ser construídas pelo método de separação de variáveis. Para aplicar este método, nós devemos procurar soluções da forma;
![]() (14)
(14)
na qual R(r) é independente da parte angular, e Y(q,f) é independente da parte radial r. Um problema análogo foi estudado na seção anterior.
Aplicando-se o procedimento de separação de variáveis, a equação de Schrödinger (eq.13) a pode ser dividida em duas equações, uma dependente da coordenada r e a outra em função da coordenadas angulares, isto é;
![]() (15)
(15)
onde ![]() é o vetor momento angular, cujo quadrado é igual a,
é o vetor momento angular, cujo quadrado é igual a,
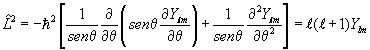
![]()
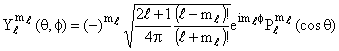
onde P´s são os polinômios de Legendre e Y´s são denominadas por harmônicos esféricos.
Neste caso
![]() .
.
Temos ainda que a solução radial é dada pela seguinte equação diferencial,
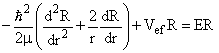 (16)
(16)
onde Vef é o potencial efetivo, dado por;
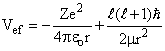 (17)
(17)
A equação (16) tem uma solução do tipo;
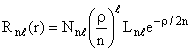 (18)
(18)
onde
![]() (19)
(19)
e Ln são os polinômios de Legendre.
Desses resultados podemos construir uma tabela para R(r), como a seguir;
|
Orbital |
n |
|
|
|
1s |
1 |
0 |
|
|
2s |
2 |
0 |
|
|
2p |
2 |
1 |
|
|
3s |
3 |
0 |
|
|
3p |
3 |
1 |
|
|
3d |
3 |
2 |
|
e as funções angulares são iguais a;
|
|
|
Função |
|
0 |
0 |
|
|
1 |
0 |
|
|
2 |
0 |
|
|
1 |
1 |
|
|
1 |
2 |
|
|
2 |
2 |
|
|
... |
... |
... |
As
funções ![]() são denominadas por esféricos
harmônicos e formam um conjunto completo de funções orto-normais,
isto é;
são denominadas por esféricos
harmônicos e formam um conjunto completo de funções orto-normais,
isto é;
![]() (20)
(20)
Os três números quânticos para o caso dos sistemas aqui estudados devem satisfazer as seguintes relações;
![]()
![]() (21)
(21)
![]()
Soluções
Esféricas e não Esféricas para Átomos Hidrogenoides
|
n |
|
|
Função de onda |
|
1 |
0 |
0 |
|
|
2
|
0 |
0 |
|
|
3 |
0 |
0 |
|
|
|
|||
|
2 |
1 |
±1 |
|
|
2 |
1 |
±1 |
|
|
2 |
1 |
0 |
|
|
|
|||
|
3 |
1 |
±1 |
|
|
3 |
1 |
±1 |
|
|
3 |
1 |
0 |
|
|
|
|||
|
3 |
2 |
0 |
|
|
3 |
2 |
±1 |
|
|
3 |
2 |
±1 |
|
|
3 |
2 |
±2 |
|
|
3 |
2 |
±2 |
|