Voltarà página principal

Leia aqui o artigo original de Schrödinger.

Aula 10

O Oscilador Harmônico

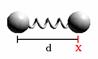
            O estudo do oscilador harmônico para sistemas microscópicos é igualmente importante ao estudo de sistemas oscilatórios macroscópicos. Em particular o movimento vibracional de dois átomos numa molécula diatômica é bem representado por um oscilador harmônico. A análise do oscilador harmônico em mecânica quântica envolve a determinação das soluções da equação de Schrödinger para uma partícula de massa m e coordenadas x movendo-se numa região onde a energia potencial V(x) tem a forma do oscilador harmônico da pela equação;

Fig.1 – Energia potencial do oscilador esboçada em função do

deslocamento das partículas

 No caso macroscópico, a constante k define a dureza da mola do oscilador.  Num sistema macroscópico a “mola” pode envolver forças elétricas ou nucleares, cuja “dureza” pode ser expressa pelo valor da constante k. Mas, como a equação de Schrödinger envolve a energia potencial do sistema, e não a força agindo sobre a partícula, é melhor pensar em k como uma constante que descreve quão bruscamente a energia potencial do sistema aumenta do seu valor de referência V = 0 na posição de equilíbrio x = 0, à medida que a partícula se fasta ponto de equilíbrio.

            A equação de Schrödinger para o oscilador harmônico pode ser re-escrita agora usando a eq. (1);  

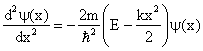                                                                    (2)

Esta é uma equação diferencial que, segundo a mecânica quântica, rege o comportamento do mesmo sistema, que a mecânica newtoniana afirma ser regido por;

                                                                                                 (3)

Agora veremos que as duas equações levam à soluções correspondentes quando elas são aplicadas a osciladores macroscópicos. Para os osciladores microscópicos, as previsões das duas equações são divergentes, e a experiência mostra que somente aquelas feitas através da equação de Schrödinger são corretas.

            Uma forma mais simples de resolver esta equação é fazendo algumas mudanças de variáveis, como a seguir; 

                                                                    (4)

Substituindo as equações (4) em (2), a equação de Schrödinger assume a forma, 

                                                                                (5)

Fazendo a mudança de variável  , tem-se que, 

                                                                                  (6) 

Usando este resultado a equação de Schrödinger pode ser re-escrita em função da nova variável s, como a seguir,

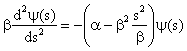                                                                           (7)

ou, 

                                                                                     (8)

onde,

                                                                        

A equação (8) é a equação de Schrödinger para o oscilador harmônico, o termo  é a freqüência de um oscilador macroscópico e conseqüentemente  é uma quantidade adimensional. Lembre-se também que, de acordo com o postulado de Born, representa a densidade de probabilidade que neste caso é a densidade de probabilidade por unidade de comprimento.

Um truque para achar a solução desta equação diferencial é obter inicialmente a solução assintótica, ou seja, a solução para valores muito grande de s e depois adaptar esta solução para que seja válida para todo valor de s, isto é

o que implica em  

                                                                                        (9)

Uma possível solução desta equação é, 

,                                                                                          (10)

onde n é um número inteiro positivo. Derivando duas vezes a equação acima com respeito a variável s, tem-se

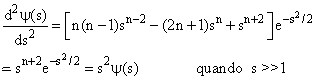                                             (11)  

Com isto vimos que a equação (9) é forma assintótica da solução procurada, a qual sugere que uma solução geral para a equação (8), válida para todos os valores de s, deve ser igual a 

 ,                                                                                   (12) 

onde H(s) é uma função a ser determinada. Substituindo a equação (12) em (8), obtém-se, 

                                                                           (13) 

onde a aspa indica a derivada com respeito a s. Agora, escrevemos H na forma de série de potência: 

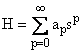                                                                                             (14)

Note que potências negativas não são permitidas neste caso, pois esta gera pontos fisicamente não aceitáveis para s=0. Então, 

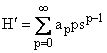                                                                                           (15)

e 

                                                     (16)

devido ao fato de que os dois primeiros termos do somatório são identicamente nulos. Substituindo as equações (14), (15) e (16) em (13), obtemos 

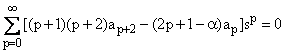                                                    (17)

Esta equação é válida para qualquer valor de s somente se o coeficiente de cada potência de s for nulo. Dai obtém-se as seguintes relações de recorrência,

                                                               (18)

Assim, por repedidas aplicações da equação (18) pode-se expressar os coeficientes de  como função de  multiplicado pelas constantes  ou dependendo se p é par ou impar, respectivamente. Com isto temos as seguintes condições de soluções fisicamente aceitáveis,

(i)                   

(ii)                          se  n é par                     e              se n é impar

Para achar solução da equação completa multiplica-se a solução da parte assintótica por um polinômio: H(s) de.

Fazendo a substituição desta solução na equação diferencial do oscilador chegamos a uma equação diferencial bem conhecida em matemática: A equação diferencial de Hermite. As soluções desta equação diferencial são os polinômios de Hermite H_v(x), que serão discutidos em outras seções.

Para que as soluções sejam aceitáveis . Neste ponto aparece o número quântico característico do oscilador harmônico n. Portanto,

  ,

onde   é a freqüência do oscilador e n = 1, 2, 3, ....

A diferença de energia entre dois níveis adjacentes para n muito grande é dada por;

  

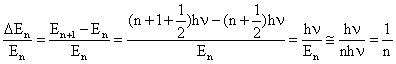
cujo valor não é suficientemente grande para ser mensurável para números quânticos grandes, que são característicos dos osciladores harmônicos macroscópicos.

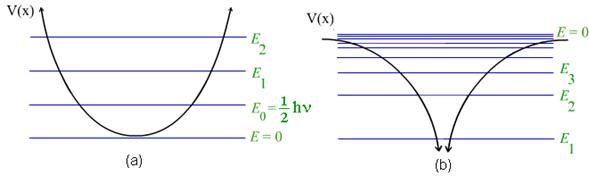
  Fig.2- Curvas de energia potencial e digramas de níveis de energia para

(a) oscilador harmônico  e (b) átomo de hidrogênio